Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
VECTOR ALGEBRA
ARIHANT PUBLICATION|Exercise Questions for Practice (Part I Basic Concepts) Very Short Answer Type Questions|15 VideosVECTOR ALGEBRA
ARIHANT PUBLICATION|Exercise Questions for Practice (Part I Basic Concepts) Short Answer Type Questions|10 VideosTHREE-DIMENSIONAL GEOMETRY
ARIHANT PUBLICATION|Exercise Chapter Practice|34 Videos
Similar Questions
Explore conceptually related problems
ARIHANT PUBLICATION-VECTOR ALGEBRA -Chapter Practice (Long Answer Type Questions)
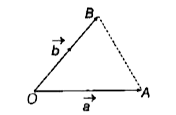
- A DeltaOAB is determined by the vectors vec(a) and vec(b) as shown in ...
Text Solution
|
- The dot product of a vector with vectors hat(i) + hat(j) - 3hat(k), ha...
Text Solution
|
- Find the unit vector perpendicular to the plane ABC, where the positio...
Text Solution
|
- If vec(b) xx vec(c) = vec(c) xx vec(a) ne vec(0), then prove that vec...
Text Solution
|
- If vec(a) = hat(i) + 4hat(j) + 2hat(k), vec(b) = 3hat(i) - 2hat(j) + 7...
Text Solution
|
- If vec(a), vec(b) and vec(c) are three vectors such that |vec(a)| = 5,...
Text Solution
|
- If vec(a) + vec(b) + vec(c) = vec(0), |vec(a)| = sqrt(37), |vec(b)| = ...
Text Solution
|
- Find the value of x such that the four points A(3, 2, 1), B(4, x, 5), ...
Text Solution
|
- If vec(a) = hat(i) + hat(j) and vec(b) = 2hat(i) - hat(k) are two vect...
Text Solution
|