Home
Class 12
PHYSICS
The variation of electrostatic potential...

The variation of electrostatic potential with radial distance r from centre of positively charged metallic thin shell of radius R is given by graph

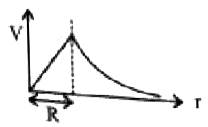
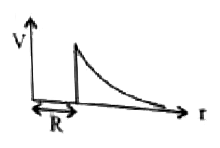
A

B

C

D

Text Solution

Verified by Experts

The correct Answer is:
A
`V_("in") = V_(s)= (KQ)/(R ) and V_("out") = (KQ)/(r ) (r gt R)`
Promotional Banner

Topper's Solved these Questions

  • ELECTROSTATIC POTENTIAL AND CAPACITANCE

    PHYSICS WALLAH|Exercise LEVEL II|34 Videos

  • ELECTROMAGNETIC WAVES

    PHYSICS WALLAH|Exercise NEET Past 5 Years Questions|8 Videos

  • GENERAL PRINCIPLES AND PROCESSES OF ISOLATION OF ELEMENTS

    PHYSICS WALLAH|Exercise NEET Past 5 Years Questions|14 Videos

Similar Questions

Explore conceptually related problems

The electrostatic field due to a point charge depends on the distance r as (l//r^(2)) . Similarly, indicates how each of the following quantities depends on r : (a) Intensity of light from a point source (b) Electrostatic potential due to a point source (c) Electrostatic potential due to a distance r from the center of a charged metallic sphere of radius R (r lt R) .

Two concentric spherical shells of radii r and R(rltR) have surface charge densities -sigma and +sigma respectively. The variation ofelectric potential V with distance x from the centre O of the shells plotted. Which of the following graphs best depict the variation qualitatively?

The dependence of electric potential V on the distance 'r' from the centre of a charged spherical shell is shown by :

The given graph shows variation (with distance r from centre) of:

The given graph shows variation (with distance r from centre) of:

Which one of the following graphs represents the variation of electric field with distance r from the centre of a charged spherical conductor of radius R?

The correct variation of gravitational potential V with radius r measured from the centre of earth of radius R is given by

The potential at a distance R//2 from the centre of a conducting sphere of radius R will be

The distance of the centre of mass of a hemispherical shell of radius R from its centre is