Home
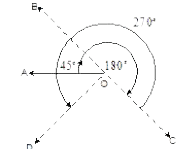
Class 10
MATHS
A man is facing West. He turns 45^(@) in...

A man is facing West. He turns `45^(@)` in the clockwise direction and then another `180^(@)` in the same direction and then `270^(@)` in the anticlockwise direction. Which direction is he facing now ?

A

South

B

North-west

C

West

D

South-west

Text Solution

Verified by Experts

The correct Answer is:
D
Clearly, the man initially faces in the direction OA. On moving 45° clockwise, he faces in the direction OB. On further moving 180° clockwise, he faces in the direction OC. Finally, on moving 270° anti-clockwise, he faces in the direction OD, which is South-west. Hence, the answer is
Promotional Banner

Similar Questions

Explore conceptually related problems

If you are facing north and turn in anti-clockwise direction, in which direction will you face ?

If the axes be turned through an angle tan^-1 2 (in anticlockwise direction), what does the equatio 4xy-3x^2=a^2 become ?

Which direction would you be facing after turning through: a. One-half of a revolution in the clockwise direction starting from North. b. Three-fourth of a revolution in the anticlockwise direction starting from South. c. One and two-fourths of a revolution in the anticlockwise direction starting from West.

Find the slope of the line, which makes an angle of 30^@ with the positive direction of Y-axis measured anticlockwise.

A vector A makes on angle 30° with the y-axis in anticlockwise direction. Another vector B makes on angle 30° with the x-axis in clockwise direction. Find angle between yectors A and B.

What is the speed of a photon with respect to another photon if (a) the two photons are going in the same direction and (b) they are going in opposite directions?

Find the slope of the line, which makes an angle of 30^o with the positive direction of y-axis measured anticlockwise.

The line 2x-y = 5 turns about the point on it, whose ordinate and abscissae are equal through an angle of 45^@ in the anti-clockwise direction. Find the equation of the line in the new position.

Let L be the line 2x+y-2=0 . The axes are rotated by 45^@ in clockwise direction then the intercepts made by the line L on the new axes are respectively

If the represented by the equation 3y^2-x^2+2sqrt(3)x-3=0 are rotated about the point (sqrt(3),0) through an angle of 15^0 , one in clockwise direction and the other in anticlockwise direction, so that they become perpendicular, then the equation of the pair of lines in the new position is