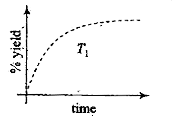
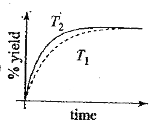
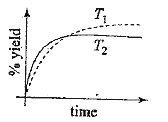
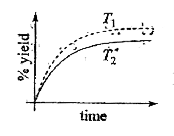
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
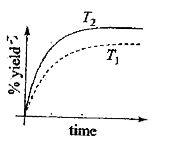
- The %yield of ammonia as a function of time in the reaction N (2) (g) ...
Text Solution
|
- The % yield of ammonia as a function of time in the reaction, N(2)(g)+...
Text Solution
|
- The prepation of SO(3)(g) by reaction SO(2)(g)+(1)/(2)O(2)(g)hArrSO(3)...
Text Solution
|
- Examine the following plots and predict whether in (i) P(1) lt P(2) "a...
Text Solution
|
- The % yield of ammonia as a function of time in the reaction N(2)(g) +...
Text Solution
|
- अभिक्रिया, N(2)(g)+3H(2)(g)leftrightarrow2NH(3)(g), DeltaH<0 में अमोनि...
Text Solution
|
- The % yield of Ammonia as a function of time in the reaction N(2)(g) +...
Text Solution
|
- At a certain temperature (T(1)) ,some hydrazine (N(2)H(4)) gas is plac...
Text Solution
|
- The prepation of SO(3)(g) by reaction SO(2)(g)+(1)/(2)O(2)(g)hArrSO(3)...
Text Solution
|