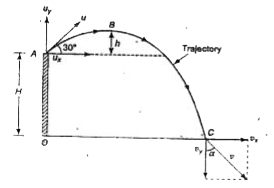
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- A ball is thrown with a velocity of 20ms^(-1) at an angle of 30^(@) ab...
Text Solution
|
- A ball is thrown from the top of tower with an initial velocity of 10m...
Text Solution
|
- A ball is projected horizontally with a velocity of 5ms^(-1) from the ...
Text Solution
|
- From the top of a building 80 m high, a ball is thrown horizontally wh...
Text Solution
|
- A ball is thrown from the top of a tower with an initial velocity of 1...
Text Solution
|
- A ball is thrown vertically upwards with a velocity of 20ms^-1 from th...
Text Solution
|
- A ball is thrown with a velocity of 30 ms^(-1) from the top of a build...
Text Solution
|
- A ball is thrown vertically upwards with a velocity of 20 ms^(-1) from...
Text Solution
|
- A ball is thrown vertically upwards with a velocity of 20 ms^(-1) from...
Text Solution
|