Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
MBD-MOTION OF SYSTEM OF PARTICLES AND RIGID BODY-EXERCISE
- A uniform square plate S (side c) and a uniform rectangular plate R (s...
Text Solution
|
- Define centre of mass.
Text Solution
|
- Under what conditions the centre of mass of two bodies lies midway bet...
Text Solution
|
- What is the relation between torque and power?
Text Solution
|
- On what factors does the moment of inertia depend?
Text Solution
|
- About which axis of a body is its moment of inertia the least?
Text Solution
|
- Why M.I. of called rotational inertia?
Text Solution
|
- Can centre of mass of a body coincide with geometrical centre of the b...
Text Solution
|
- If the ice on the polar caps of the earth melts, how will it affect th...
Text Solution
|
- Two satellites of equal masses are revolving around at different heigh...
Text Solution
|
- How will you distinguish between a hard boiled egg and a raw egg by sp...
Text Solution
|
- Prove that: tau = I alpha
Text Solution
|
- Prove that: L = I omega
Text Solution
|
- State the principle of conservation of angular momentum.
Text Solution
|
- Define centre of mass.
Text Solution
|
- A stone tied to one end of string is moved in a circle. How much work ...
Text Solution
|
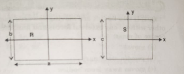 Show that `I_(yR`//I_(yS) < 1`
Show that `I_(yR`//I_(yS) < 1`