Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
MBD-GRAVITATION-EXERCISE
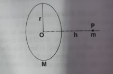
- A mass m is placed at P a distance h along the normal through the cent...
Text Solution
|
- What is the difference between gravity and gravitation?
Text Solution
|
- How g and G are related?
Text Solution
|
- Is the density of earth uniform throughout?
Text Solution
|
- When a pendulum is taken to a mountain, it becomes slow, but a wrist w...
Text Solution
|
- Imagine a spacecraft going from earth to the moon. HOw does its weight...
Text Solution
|
- What will be the weight of a body at the centre of the earth?
Text Solution
|
- Does the value of 'g' vary, as we move on the surface of earth?
Text Solution
|
- Establish the relation between 'g' and 'G' .
Text Solution
|
- Write four important properties of inertial mass.
Text Solution
|
- What happens to the weight of a body when it is taken to a mountain pe...
Text Solution
|
- State the universal law of gravitation.
Text Solution
|
- Prove that the force of gravitation obeys Newton's thrid law of motion...
Text Solution
|
- Show that intensity of gravitational field is equal to acceleration d...
Text Solution
|
- Define gravitational potential energy. Find the expression for gravita...
Text Solution
|