Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
MBD-MECHANICAL PROPERTIES OF SOLIDS-EXERCISE
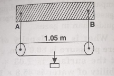
- A rod of length 1.05 m having negligible mass is supported at its ends...
Text Solution
|
- On what factors, the modulus of elasticity depends?
Text Solution
|
- On what factors, the modulus of elasticity depends?
Text Solution
|
- Two wires of different materials are suspended from a rigid support. T...
Text Solution
|
- Why springs are made of steel and not of copper?
Text Solution
|
- An elastic wire is cut to half its original length. How would it affec...
Text Solution
|
- What is an elastomer?
Text Solution
|
- Distinguish between elasticity and plasticity.
Text Solution
|
- Elasticity has different meaning in physics and in our daily life. Com...
Text Solution
|
- A wire stretches by a certain amount under a load. If the load and rad...
Text Solution
|
- Steel is more elastic than rubber. Explain why?
Text Solution
|
- When is a body called elastic and when is it called plastic? Explain e...
Text Solution
|
- Draw stress-strain curve for aa loaded steel wire and hence define te ...
Text Solution
|
- Define Young's modulus of elasticitiy. normal stress and longitudinal ...
Text Solution
|
- Derive an expression for the electric potential at a point along the a...
Text Solution
|