Similar Questions
Explore conceptually related problems
Recommended Questions
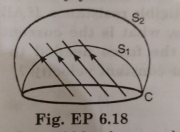
- Consider a closed loop C in a magnetic field (Fig. EP 6.18). The flux ...
Text Solution
|
- Consider a closed loop C in a magnetic field, Fig. The flux passing th...
Text Solution
|
- Assertion If a loop is placed in a non-uniform (with respect to positi...
Text Solution
|
- A square loop of edge 'a' carries a current l. The magnetic field at t...
Text Solution
|
- A rectangular loop of area 0.2m^(2) is lying in a magnetic field of 5x...
Text Solution
|
- A rectangular loop of area 0.4m^(2) is lying in a magnetic field of 4x...
Text Solution
|
- When a 10 muC charge is enclosed by a closed surface, the flux passing...
Text Solution
|
- The magnetic field perpendicular to the plane of a loop of area 0.1m^(...
Text Solution
|
- At the Earth's equator, B is horizontal and to the north, with a magni...
Text Solution
|