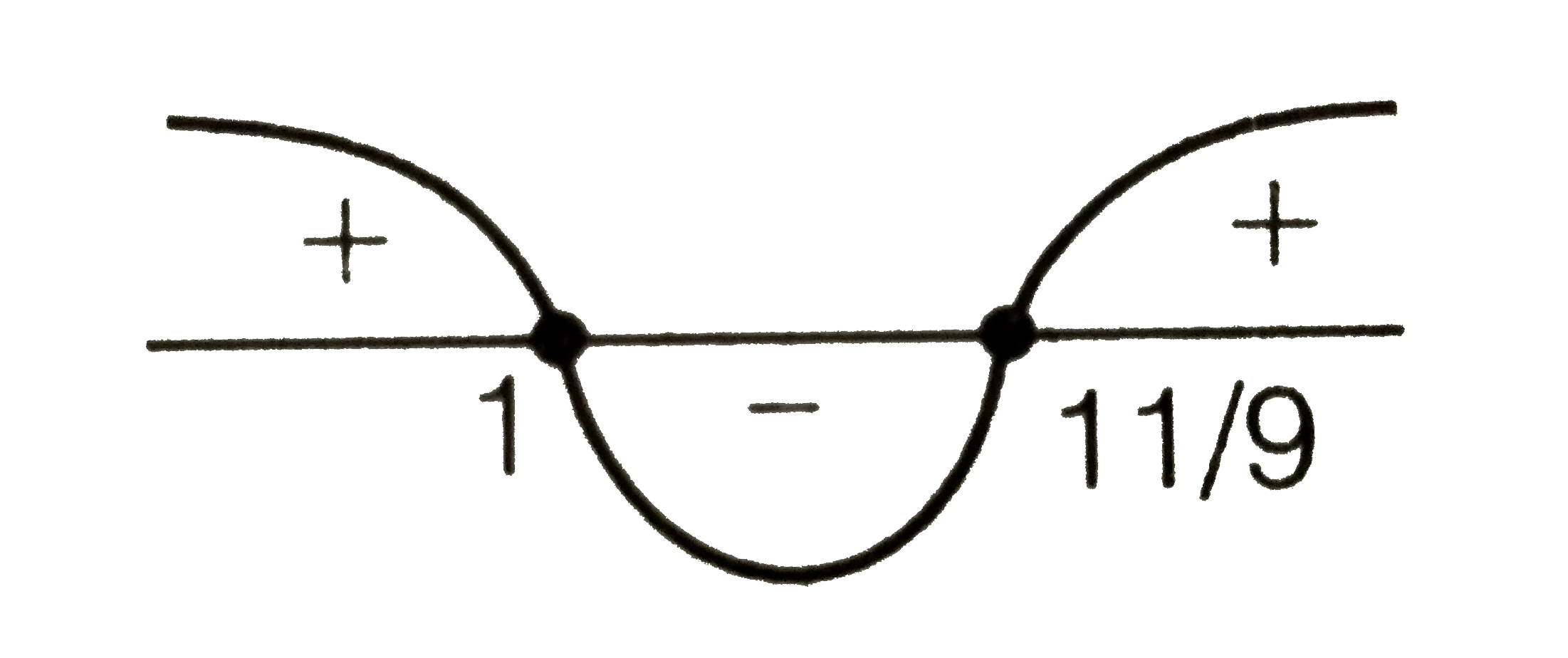
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- For what values of m epsilonR, both roots of the equation x^(2)-6mx+9m...
Text Solution
|
- If x=2 andx=3 are roots of the equation 3x^2-2k x+2m=0, find the va...
Text Solution
|
- If both roots of the equation x^(2)+x+a=0 exceeds 'a' then
Text Solution
|
- If both roots of the equation x^(2)-(m-3)x+m=0 (m epsilonR) are posit...
Text Solution
|
- यदि x=2 और x=3 समीकरण 3x^(2)-2kx+2m=0 के मूल हों, तो k और m का मान ज्ञ...
Text Solution
|
- For what value of m the roots of the equation x^2-2(5+2m)x+3(7+10m)=0...
Text Solution
|
- The integral value of m for which the quadratic equation (2m-3)x^2-4x+...
Text Solution
|
- equation for what value of m 2mx^(2)-2(1+2m)x(3+2m)=0 The origin will ...
Text Solution
|
- m in R के किस मान के लिए समीकरण x^2-6mx+9m^2-2m+2=0 के मूल 3 से बड़े...
Text Solution
|