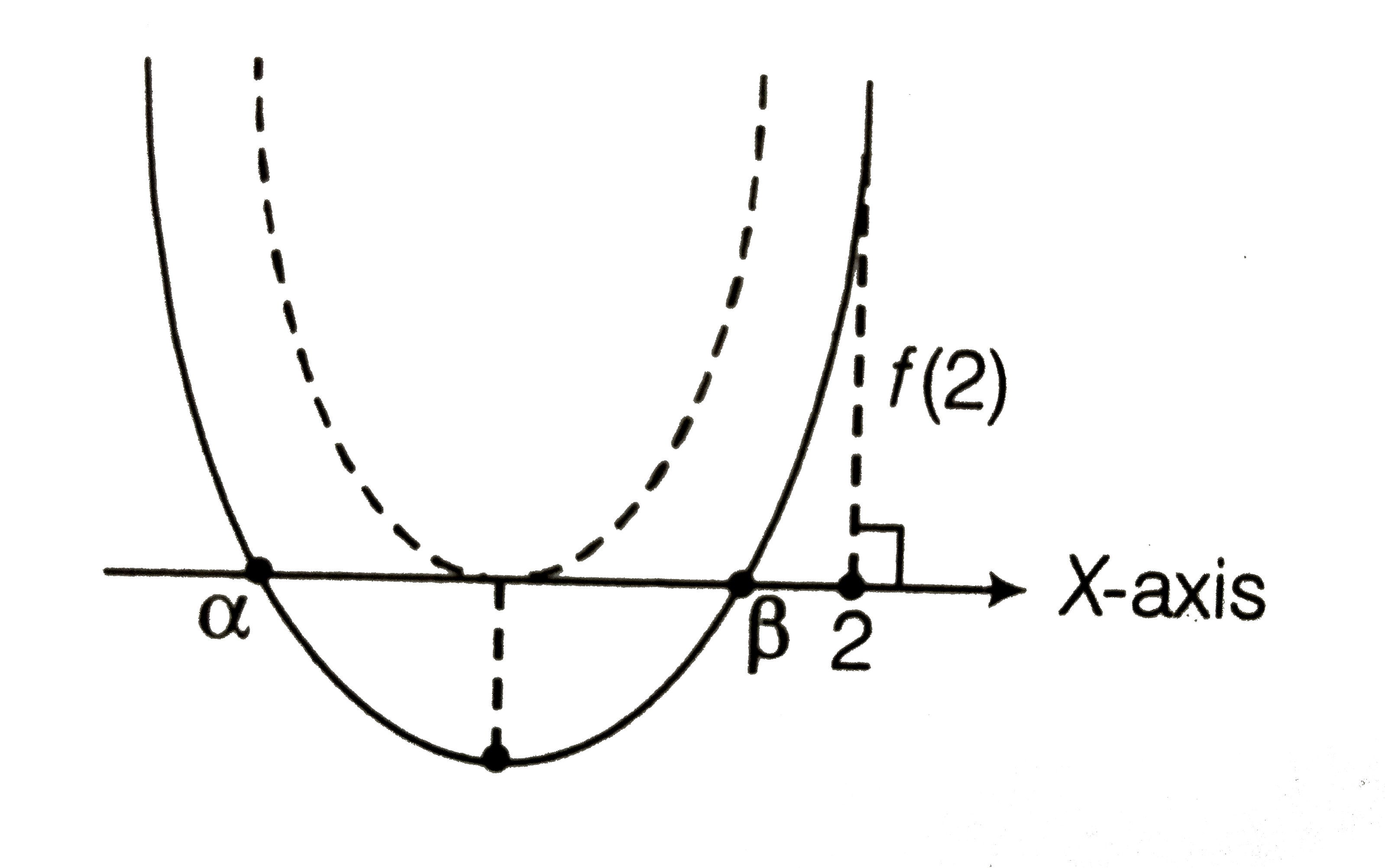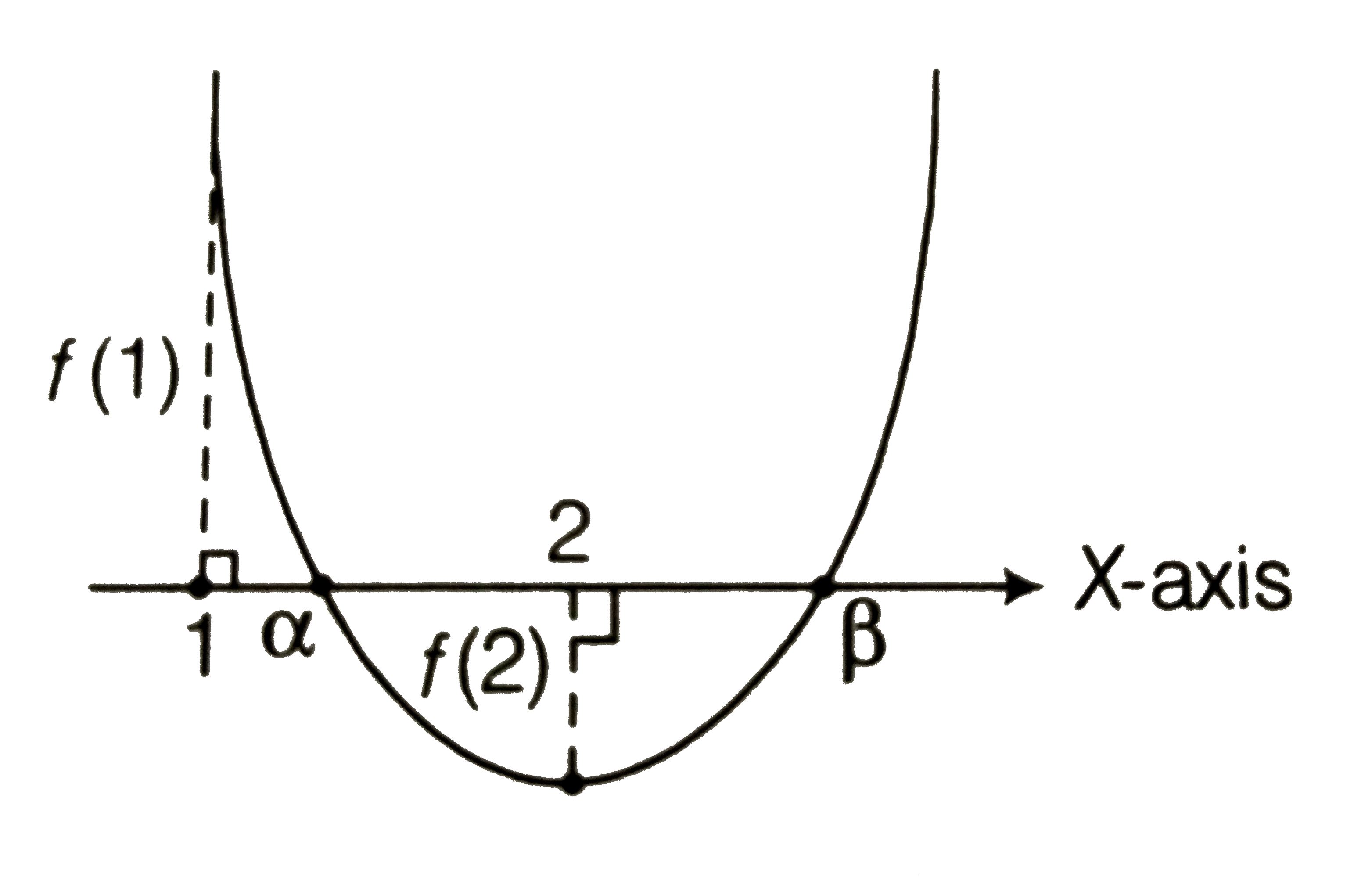Let `x^2-(m-3)x+m=0 (m in R)` be a quadratic equation . Find the values of m for which the roots are:
(ix)one root is smaller than 2 & other root is greater than 2
(x) both the roots are greater than 2.
(xi) both the roots are smaller than 2.
(xii) exactly one root lies in the interval (1,2)
(xiii) both the roots lies in the interval (1,2)
(xiv) at least one root lies in the interval (1,2)
(xv) one root is greater than 2 and the other root is smaller than 1

Explanation

Let `f(x)=x^(2)-(m-3)x+m`
Here `a=1, b=-(m-3),c=m`
and `D=b^(2)-4ac=(m-3)^(2)-4m`
`=m^(2)-10m+9=(m-1)(m-9)`
and `x`-x coordinate of vertex `=-b/(2a)=((m-3))/2`
(i) Both the roots are smaller than 2 `Dge0`

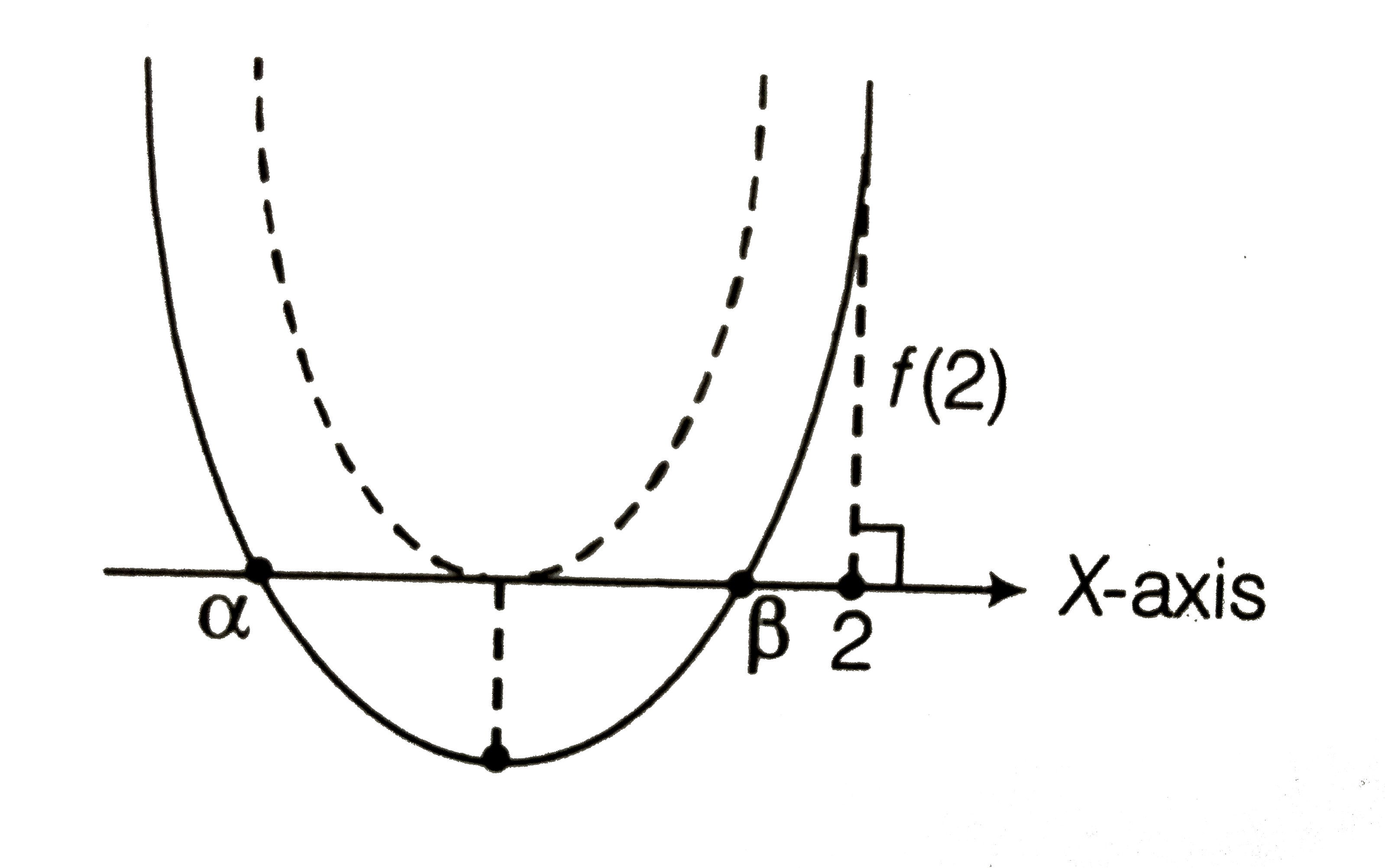
i.e. `(m-1)(m-9)ge0`
`:.m epsilon(-oo1[uu[9,oo)` ............i
`f(2)gt0`
i.e. `4-2(m-3)+mge0`
`impliesmlt10`
`:.m epsilon(-oo,10)`......ii and `x`- coordinate of vertex `lt2`
i.e. `((m-3))/2ltimpliesmlt7`
`:.m epsilon(-oo,7)` iii
On combining Eqs.i,ii, and iii we get
`m epsilon (-oo,1]`
(ii) Both the roots are greater than 2 `Dge0`

i.e. `(m-1)(m-9)ge0`
`:.m epsilon(-oo,1]epsilon[9,oo)`.........i
`f(2)gt0`
i.e. `4-2(m-3)+mgt0`
`impliesm lt 10`......ii
and x-coordinate of vertex `gt2`
i.e. `((m-3))/2gtimpliesmlt7`
`:. m epsilon(7,oo)` .....iii
On combining Eqs. i, ii and iii we get
`m epsilon[9,10)`
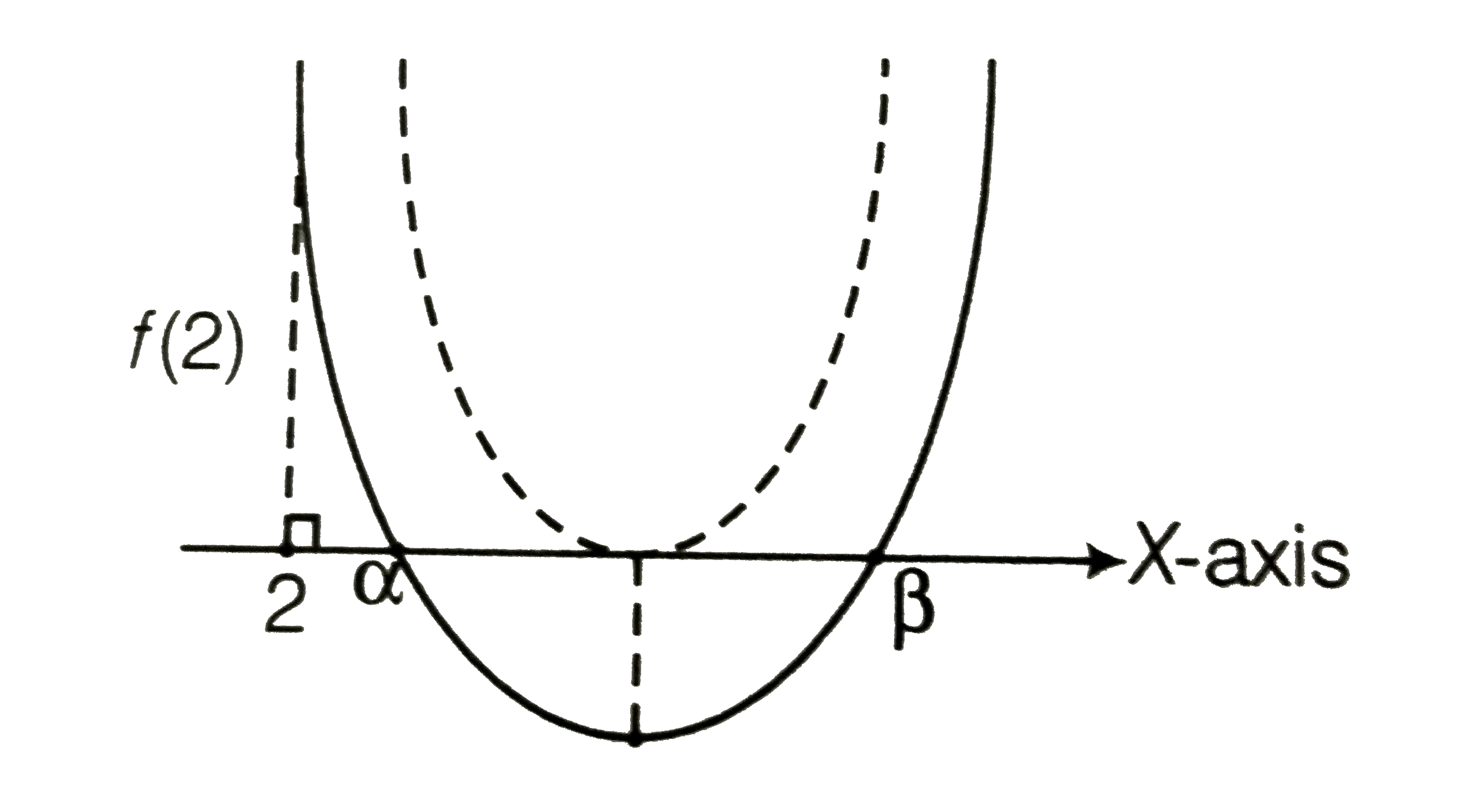
(iii) One root is smaller than 2 and the other root is greater than 2
`Dlt0`

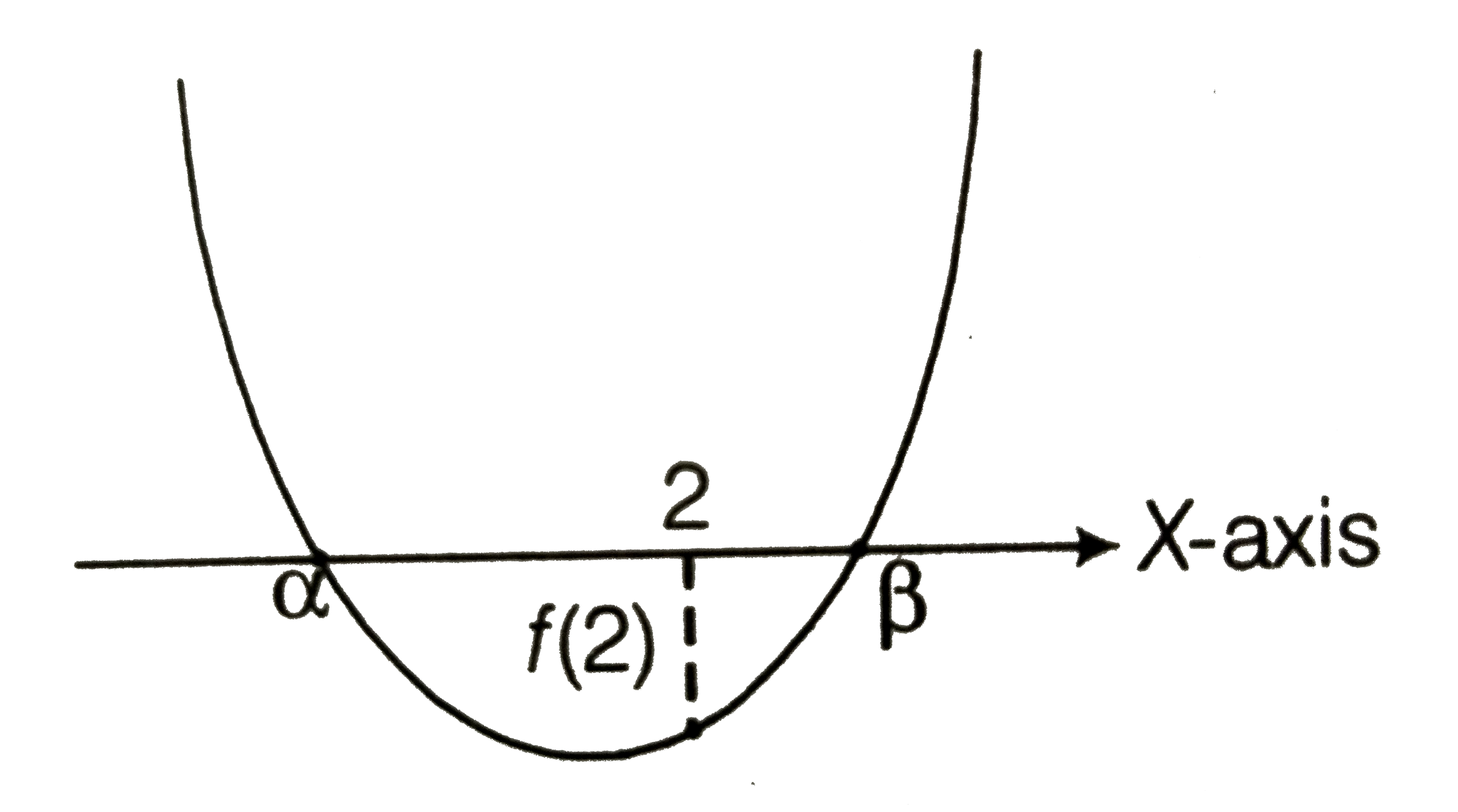
i.e. `(m-1)(m-9)gt0`
`:.m epsilon (-oo,1)uu(9,oo)`....i
`f(2)lt0`
i.e `4-2(m-3)+mlt0`
`:.mgt10`
`:.m epsilon (10,oo)`....ii
On combining Eqs i and ii we get
` m epsilon (10,oo)`
(iv) Exactly one root lies in the interval (1,2)
`Dgt0`

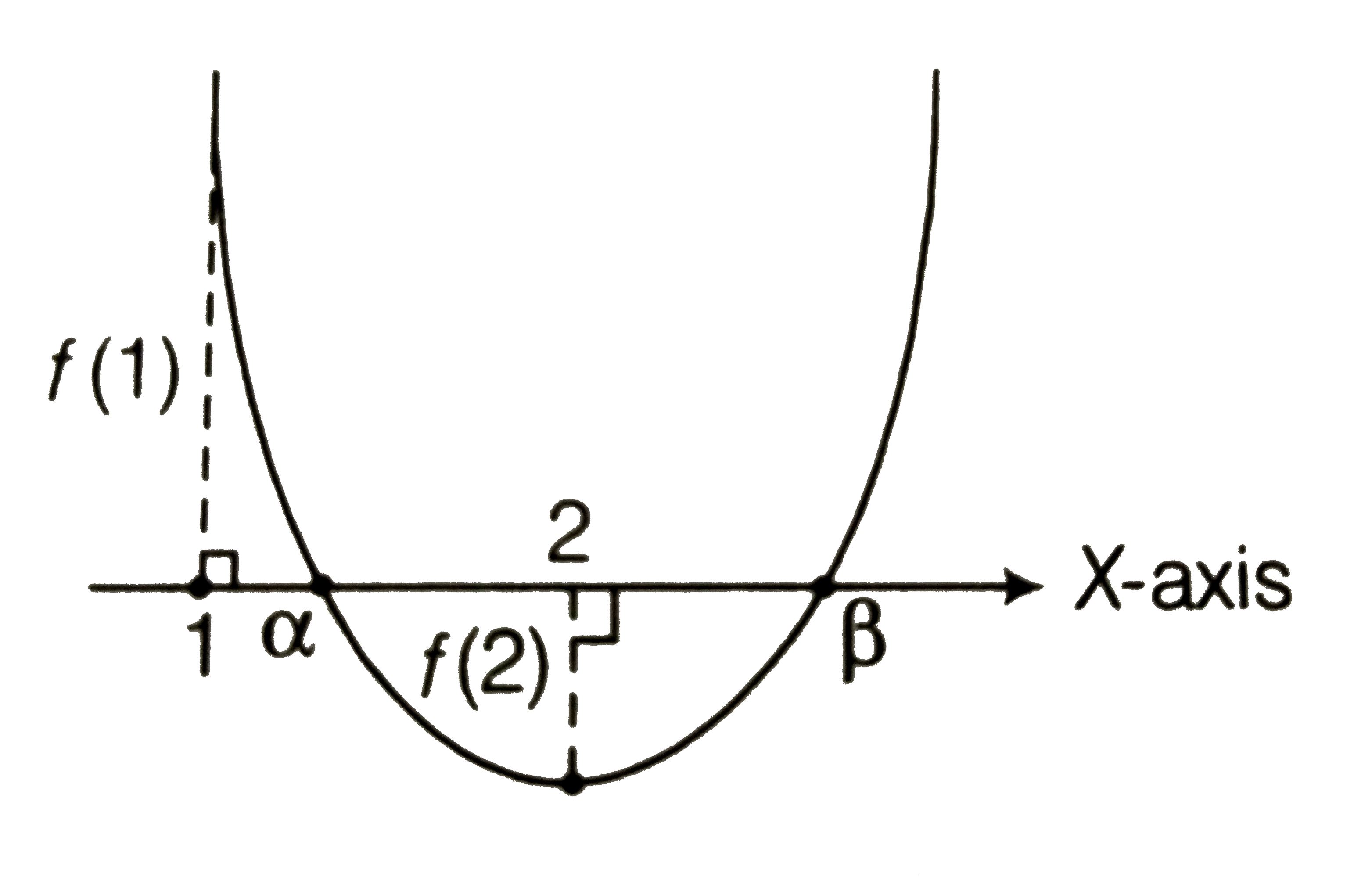
i.e., `(m-1)(m-9)gt0`
`:. m epsilon (-oo,1)uu(9,oo)`...i
`f(1)f(2)lt0`
`(1-(m-3)+m)(4-2(m-3)+m)lt0`
`implies4(-m+10)lt0`
`impliesm-10gt0impliesmgt10`
`:.m epsilon (10,oo)` ....ii
On combining Eqs (i) and (ii) we get
` m epsilon (10,oo)`
(v) Both the roots lie in the interval (1,2)
`Dge0`

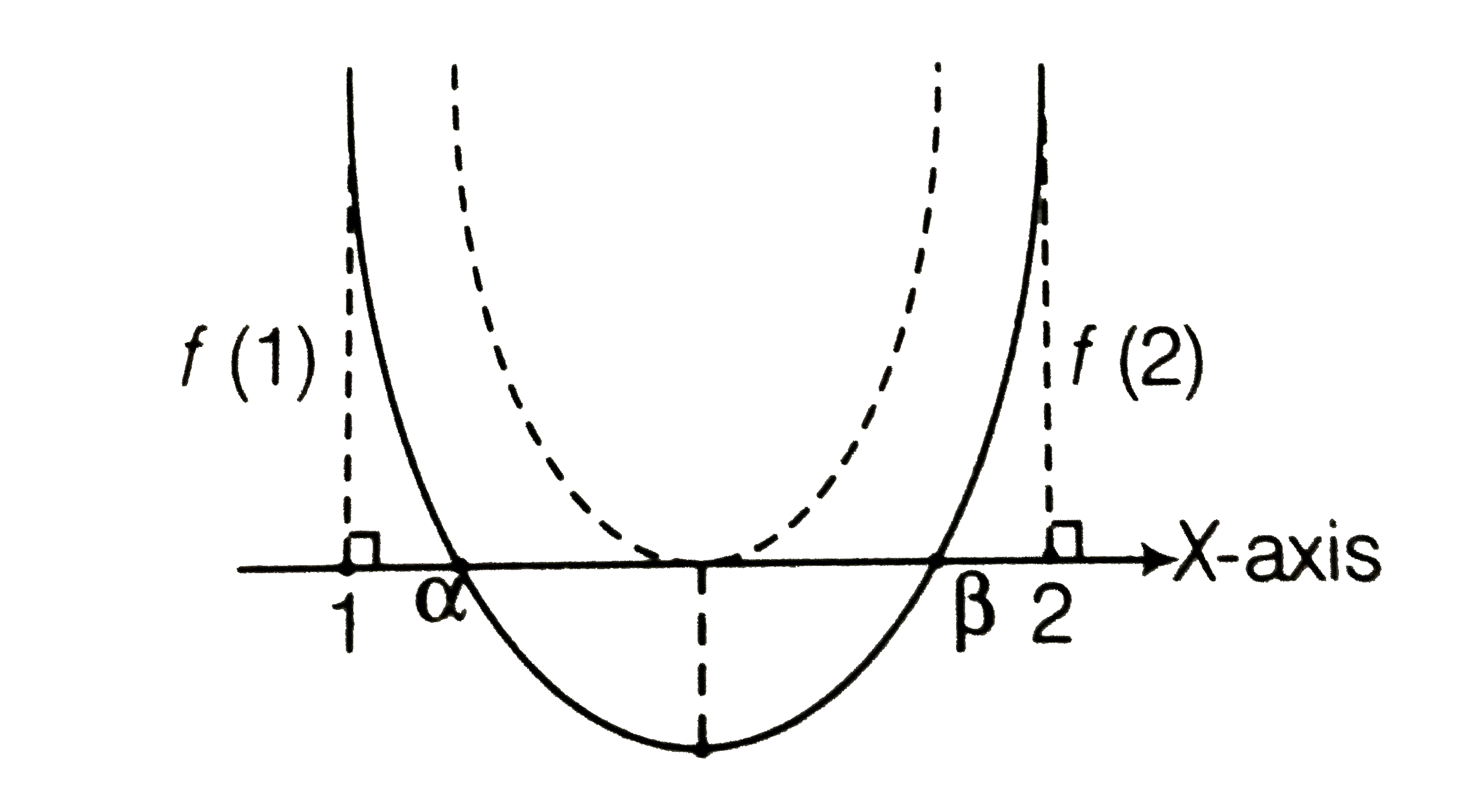
i.e. `(m-1)(m-9)ge0`
`:. m epsilon (-oo,1]uu[9,oo)`...i
`f(1)gt0`
i.e. `(1-(m-3)+m)gt0implies4gt0`
`:.mepsilonR`.ii
`f(2)gt0`
i.e. `4-2(m-3)+mgt0impliesmlt10`
`:.m epsilon (-oo,10)`..iii
`1ltx` coordinate of vertex `lt2`
i.e. `1lt((m-3))/2lt2`
`implies2ltm-3lt4` or `5ltmlt7`
`:.m epsilon (5,7)`.iv
On combining Eqs. i,ii,iii and iv we get
`m epsilon phi`
(vi) One root is greater than 2 and the other root is smaller than `1 Dgt0`

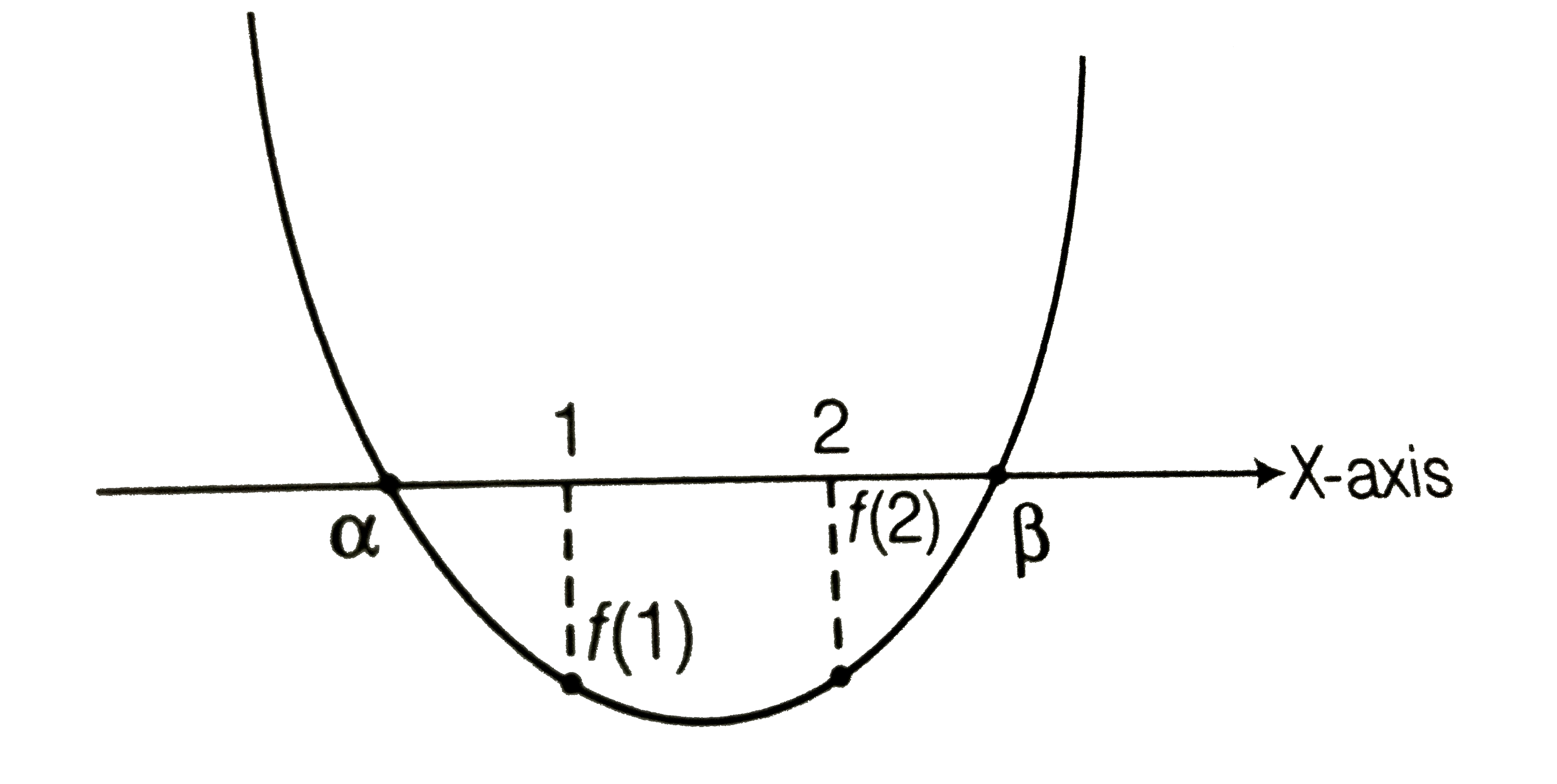
i.e. `(m-1)(m-9)gt0`
`:.m epsilon (-oo,1)uu(9,oo)`.i
`f(1)lt0`
i.e. `4lt0` which is not possible.
Thus , no such `m` exists.
(vii) At least one root lie in the interval (1,2)
Case I Exactly one root lies in (1,2)
`mepsilon(10,oo)` [from (iv) part]
Case II Both roots lie in the interval (1,2).
`m epsilon (10,oo)`
(viii) Atleast one root is greater than 2
Case I One root is smaller than 2 and the other root is greater than 2.
Then, `m epsilon(10,oo)` [from iii) part]
Case II Both the roots are greaters than 2 then `m epsilon [9,10)`.
Hence atleast one root is greater than 2.
`:.m epsilon (10,oo)uu[9,10)` or `m epsilon [9,10)uu(10,oo)`