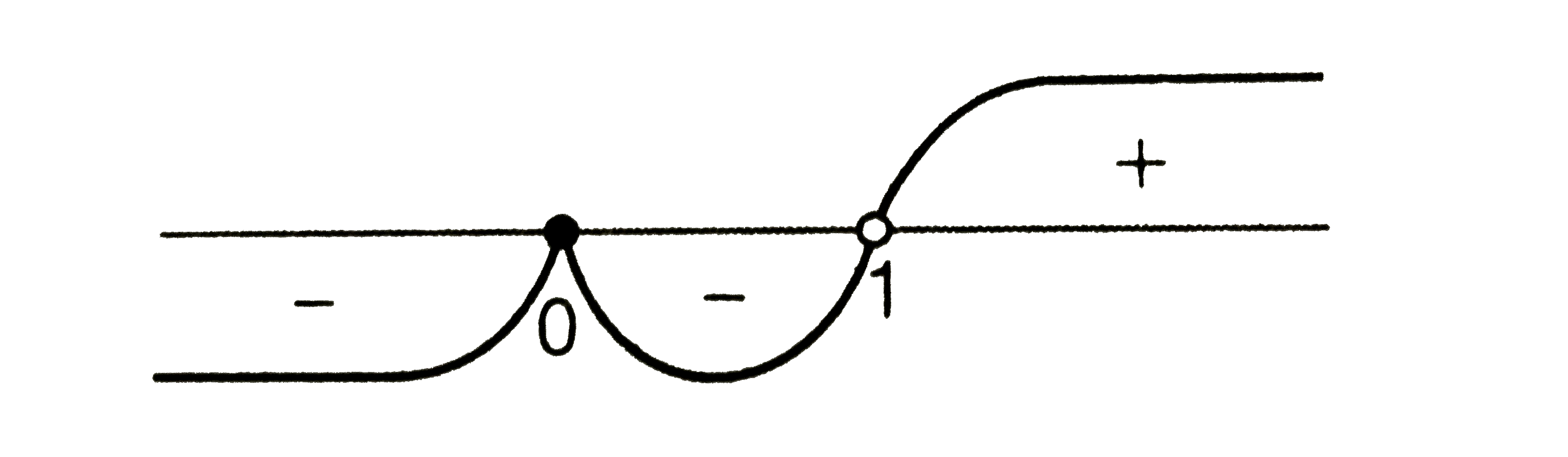
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Solve the equation |x/(x-1)|+|x|=x^2/|x-1|
Text Solution
|
- Solve the equation x(x+2)(x^2-1)=-1.
Text Solution
|
- Solve the equation: |x+1|-|x|+3|x-1|-2|x-2|=x+2
Text Solution
|
- Solve the following equations : 2((x)/(x+1))^(2)-5((x)/(x+1))+2=0\ xne...
Text Solution
|
- समीकरण (1)/(x + 1) + (2)/(x +2) = (4)/(x + 4) x != -1, -2, -4 को हल की...
Text Solution
|
- Solve the equations : ((x+1)^(3)-(x-1)^(3))/((x+1)^(2)-(x-1)^(2))=2
Text Solution
|
- समीकरण (x+1)/(x) + (x)/(x+1) = (5)/(2) को हल कीजिये -
Text Solution
|
- समीकरण (x+1)/(x) + (x)/(x+1) = (5)/(2) को हल कीजिये।
Text Solution
|
- समीकरण (x+1)/(x) + (x)/(x+1) = (5)/(2) को हल कीजिये।
Text Solution
|