Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
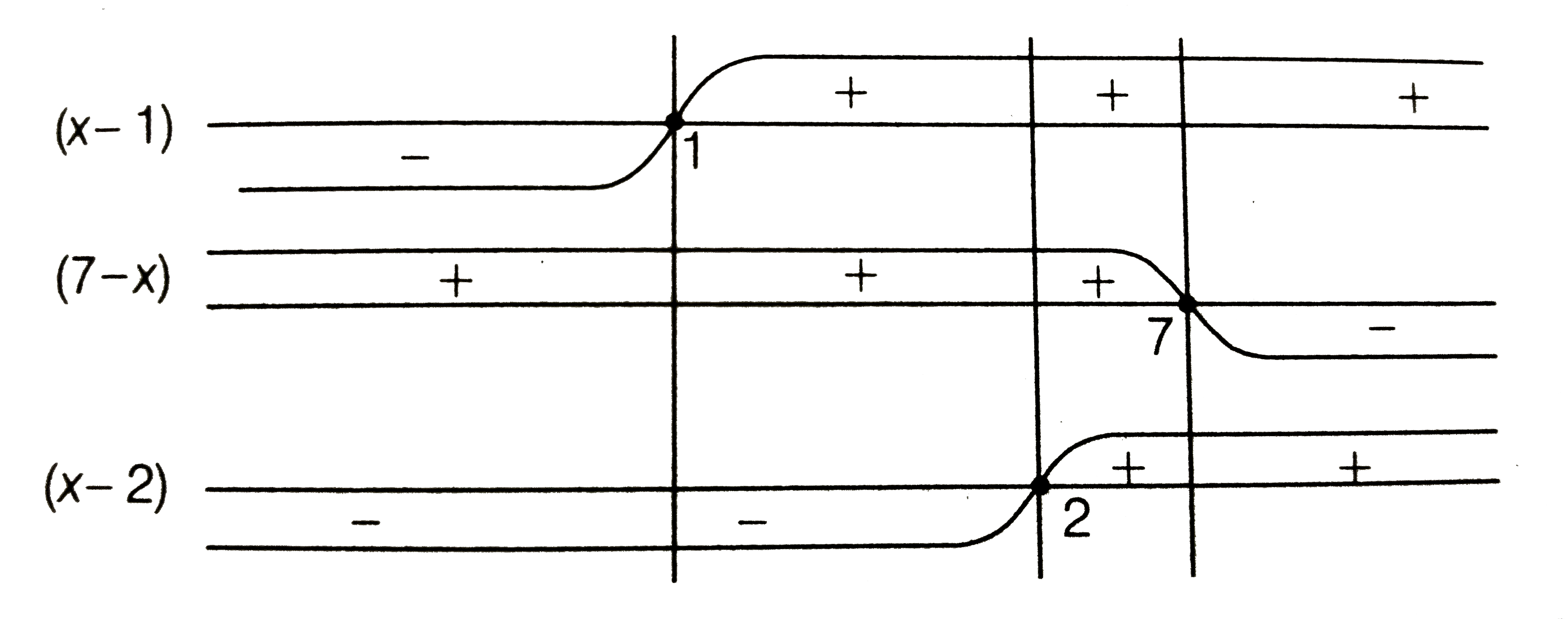
- Solve the equation |x-1|+|7-x|+2|x-2|=4
Text Solution
|
- Solve the following equations: log(7)(2^(x)-1)+log(7)(2^(x)-7)=1
Text Solution
|
- Solve: ((4+x)(5-x))/((2+x)(7-x))=1
Text Solution
|
- समीकरण (1)/(x + 1) + (2)/(x +2) = (4)/(x + 4) x != -1, -2, -4 को हल की...
Text Solution
|
- Solve : (x-4)(x-7)(x-2)(x+1)=16
Text Solution
|
- इन समीकरण को हल कीजिये tan^(-1)""(x-2)/(x-4)+tan^(-1)""(x+2)/(x+4)=pi...
Text Solution
|
- Solve the equation 2(x+2)-3(x-3)=x+7
Text Solution
|
- தீர்க்க : (x-4)(x-7)(x-2)(x+1)=16
Text Solution
|
- Solve the equation. x-2=7
Text Solution
|