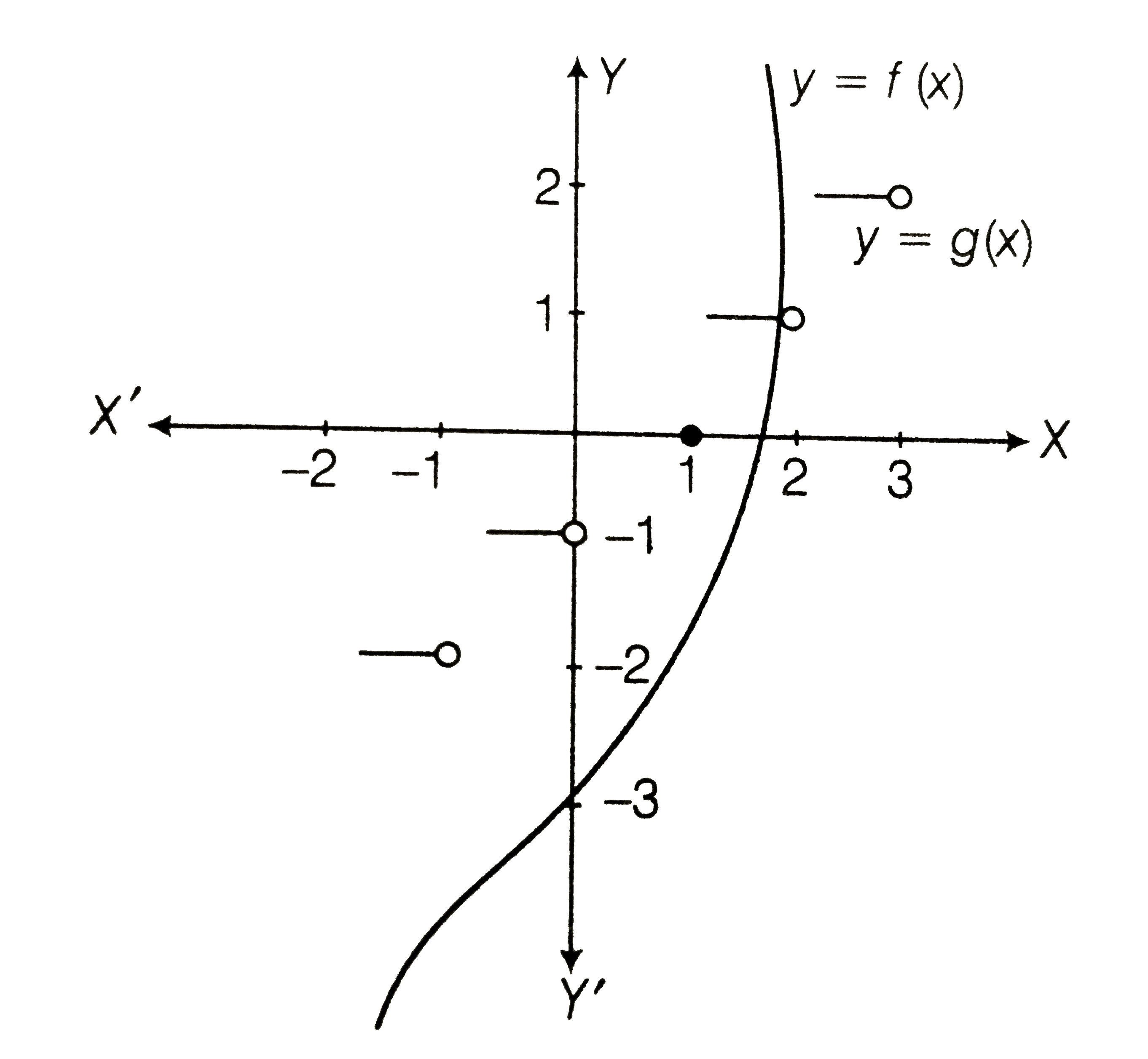
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Solve the equation x^(3)-[x]=3, where [x] denotes the greatest integer...
Text Solution
|
- Find all the points of discontinuity of the greatest integer function...
Text Solution
|
- lim(x rarr a(-)){(|x|^(3))/(a)-[(x)/(a)]^(3)},(a<0) where [x] denotes ...
Text Solution
|
- Number of points of discontinuity of f(x)=(2x^(3)-5] in [1,2) is equal...
Text Solution
|
- Let [x] denote the greatest integer less than or equal to x. If x=(sqr...
Text Solution
|
- The function of f:R to R, defined by f(x)=[x], where [x] denotes the g...
Text Solution
|
- lim(xrarr oo) (log[x])/(x) , where [x] denotes the greatest integer le...
Text Solution
|
- Find all the points of discontinuity of the greatest integer function ...
Text Solution
|
- Solve the following equations x^(2)-3-{x}=0 where [x] denotes the grea...
Text Solution
|