for what values of m, the equation ` 2x^(2) -2 ( 2m +1) x+ m ( m +1) = 0, m in R` has
(i) Both roots smallar than 2 ?
(ii) Both roots greater than 2 ?
(iii) Both roots lie in the interval (2,3) ?
(iv) Exactly one root lie in the interval (2,3) ?
(v) One root is smaller than 1, and the other root is greater than 1 ?
(vi) One root is greater than 3 and the other root is smaller than 2 ?
(vii) Roots ` alpha and beta` are such that both 2 and 3 lie between `alpha and beta ` ?
for what values of m, the equation ` 2x^(2) -2 ( 2m +1) x+ m ( m +1) = 0, m in R` has
(i) Both roots smallar than 2 ?
(ii) Both roots greater than 2 ?
(iii) Both roots lie in the interval (2,3) ?
(iv) Exactly one root lie in the interval (2,3) ?
(v) One root is smaller than 1, and the other root is greater than 1 ?
(vi) One root is greater than 3 and the other root is smaller than 2 ?
(vii) Roots ` alpha and beta` are such that both 2 and 3 lie between `alpha and beta ` ?
(i) Both roots smallar than 2 ?
(ii) Both roots greater than 2 ?
(iii) Both roots lie in the interval (2,3) ?
(iv) Exactly one root lie in the interval (2,3) ?
(v) One root is smaller than 1, and the other root is greater than 1 ?
(vi) One root is greater than 3 and the other root is smaller than 2 ?
(vii) Roots ` alpha and beta` are such that both 2 and 3 lie between `alpha and beta ` ?
Text Solution
Verified by Experts
The correct Answer is:
(i) `m epsilong (-oo,(7-sqrt(3))/2)` (ii) `m epsilon ((7+sqrt(33))/2,oo)` (iii) `m epsilon phi`
(iv) `m epsilon ((7-sqrt(3))/2,(11-sqrt(73))/2)uu((7+sqrt(33))/2,(11+sqrt(73))/2)`
(v) `m epsilon (0,3)` (vi) `m epsilon ((7-sqrt(3))/2,(7+sqrt(33))/2)`
(vii) `m epsilon ((7-sqrt(33))/2,(11-sqrt(73))/2)uu((7+sqrt(33))/2,(11+sqrt(73))/2)`
(viii) `m epsilon ((7-sqrt(3))/2,(7+sqrt(33))/2)uu((7+sqrt(3))/2,oo)`
(ix) `m epsilon (-oo,(7-sqrt(33))/2)uu((7-sqrt(33)/2,(7+sqrt(33))/2)`
(x) `m epsilon `((11-sqrt(73))/2,(7+sqrt(3))/2)`
(iv) `m epsilon ((7-sqrt(3))/2,(11-sqrt(73))/2)uu((7+sqrt(33))/2,(11+sqrt(73))/2)`
(v) `m epsilon (0,3)` (vi) `m epsilon ((7-sqrt(3))/2,(7+sqrt(33))/2)`
(vii) `m epsilon ((7-sqrt(33))/2,(11-sqrt(73))/2)uu((7+sqrt(33))/2,(11+sqrt(73))/2)`
(viii) `m epsilon ((7-sqrt(3))/2,(7+sqrt(33))/2)uu((7+sqrt(3))/2,oo)`
(ix) `m epsilon (-oo,(7-sqrt(33))/2)uu((7-sqrt(33)/2,(7+sqrt(33))/2)`
(x) `m epsilon `((11-sqrt(73))/2,(7+sqrt(3))/2)`
`:'2x^(2)-2(2m+1)x+m(m+1)=0 [:'m epsilonR]`
`:.D=[-2(2m+1)]^(2)-8m(m+1)[D=b^(2)-4ac]`
`=4{(2m+1)^(2)-2m(m+1)}`
`=4(2m^(2)+2m+1)`
`=8(m^(2)+m+1/2)=8{(m+1/2)^(2)+1/4}gt0`
or `D gt0, AA m epsiolonR`……i
x coordinate of vertex `=-b/(2a)=(2(m+1))/4=(m+1/2)`.....ii
and let
`f(x)=x^(2)-(2m+1)x+1/2m(m+1)` ...........iii
(i) Both roots are smaller than 2.

Consider the following cases:
Case I `Dge0`
`:. m epsilonR` [from Eq. (i) ]
CaseII x-coordinate of vertex `lt2`.
`impliesm+1/2lt0` [from Eq. (ii) ]
or `mlt3/2`
Case III `f(2)gt0`
`implies4-(2m+1)2+1/2m(m+1)gt0`
`impliesm^(2)-7m+4gt0`
`:.m epsilon(-oo,(7-sqrt(3))/2)uu((7+sqrt(33))/2,oo)`
Combining all cases we get
`m epsilon (-oo,(7-sqrt(3))/2)`
(ii) Both roots are greater than 2.
Consider the following cases.
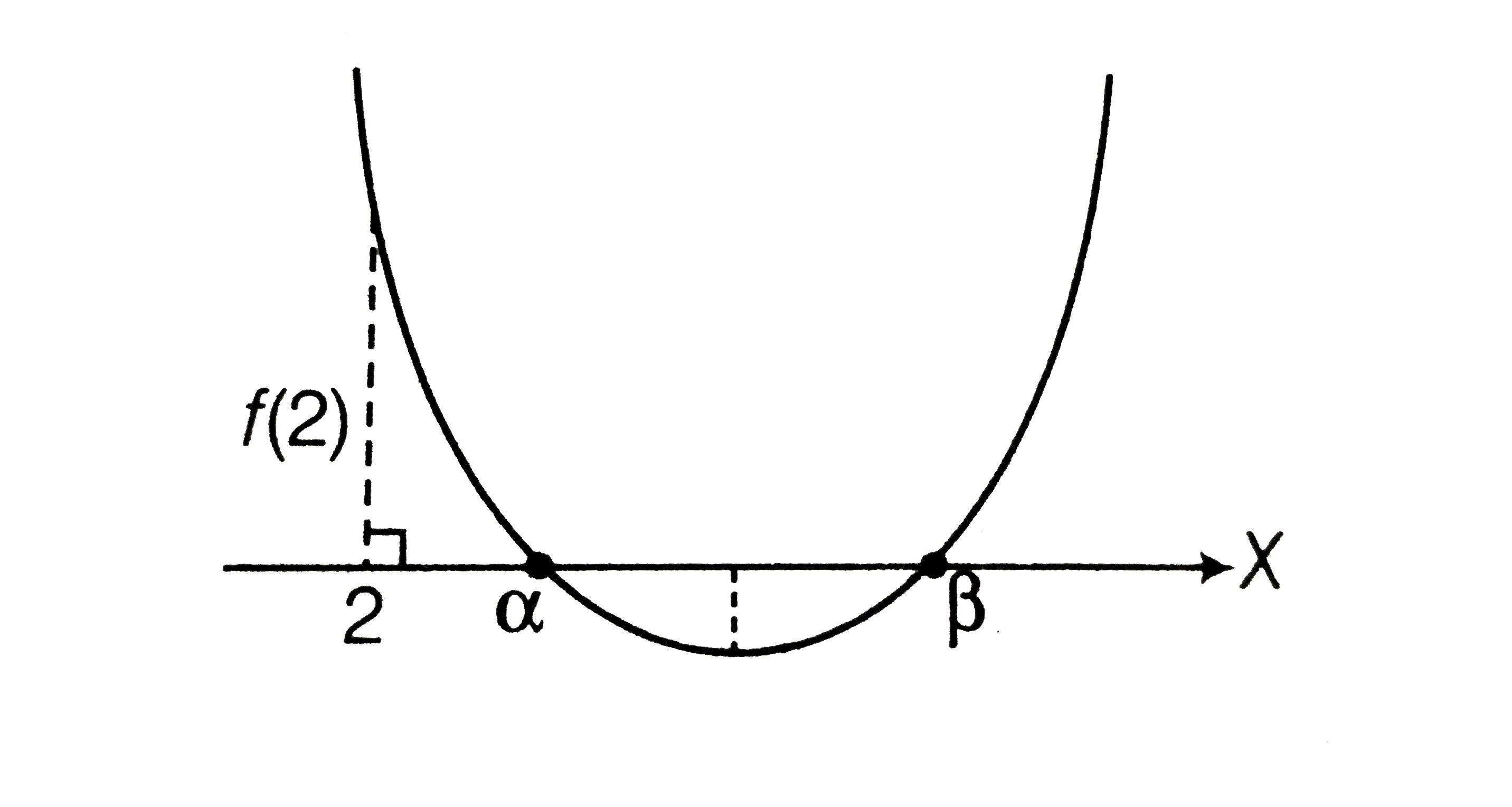
Case I `Dge0`
`:. m epsilon R`[from Eq. (i)]
Case II x- coordinate of vertex `gt2`
`impliesm+1/2gt2`[ from Eq. (ii)]
`:.m gt3/2`
Case III `f(2)gt0`
`m epsilon (-oo,(7-sqrt(33))/2)uu(7+(sqrt(33))/2,oo)` [from part (a) ]
Combining all cases, we get
`m epsilon ((7+sqrt(33))/2,oo)`
(iii) Both roots lie in the interval (2,3).
Consider the following cases:

CAse I `Dge0`
`:. m epsilonR` [from Eq. (i)]
Case II `f(2)gt0`
`:. m epsilon (-oo,(7-sqrt(3))/2)uu((7+sqrt(33))/2,oo)` [from part (a)]
Case Case III `f(3)gt0`
`implies9-3(2m+1)+1/2m(m+1)gt0`
or `m^(2)-11m+12gt0`
`:m epsilon (-oo,(11-sqrt(73))/2)uu((11+sqrt(73))/2,oo)`
Case IV `2ltx` -coordinate of vertex `lt3`
`implies2ltm+1/2lt3`
or `3/2ltmlt5/2` or `m epsilon (3/2,5/2)`
Combining allcases we get
`m epsilon phi`
(iv) Exactly one root lie in the interval (2,3).
Consiser the following cases:
Case I `Dgt0`
`:.m epsilon R` [from Eq (i) ]
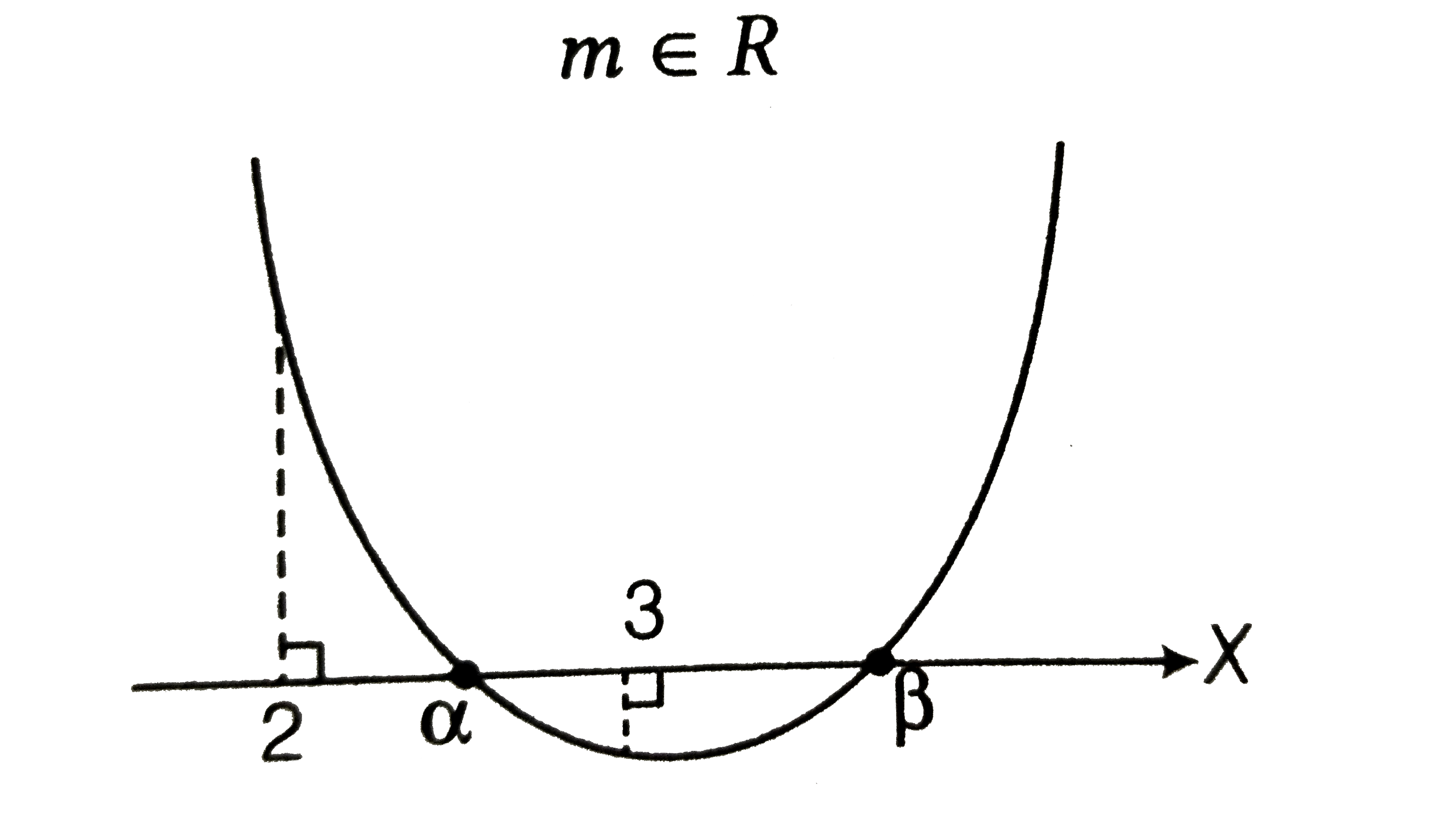
Case II `f(2)f(3)lt0`
`(4-2(2m+1)+1/2m(m+1))`
`(9-3(2m+1)+1/2m(m+1))lt0`
`implies(m^(2)-7m+4)(m^(2)-11m+12)lt0`
`implies(m-(7-sqrt(33))/2)(m-(7+sqrt(33))/2)`
`(m-(11-sqrt(73))/2)(m-(11+sqrt(73))/2)lt0`
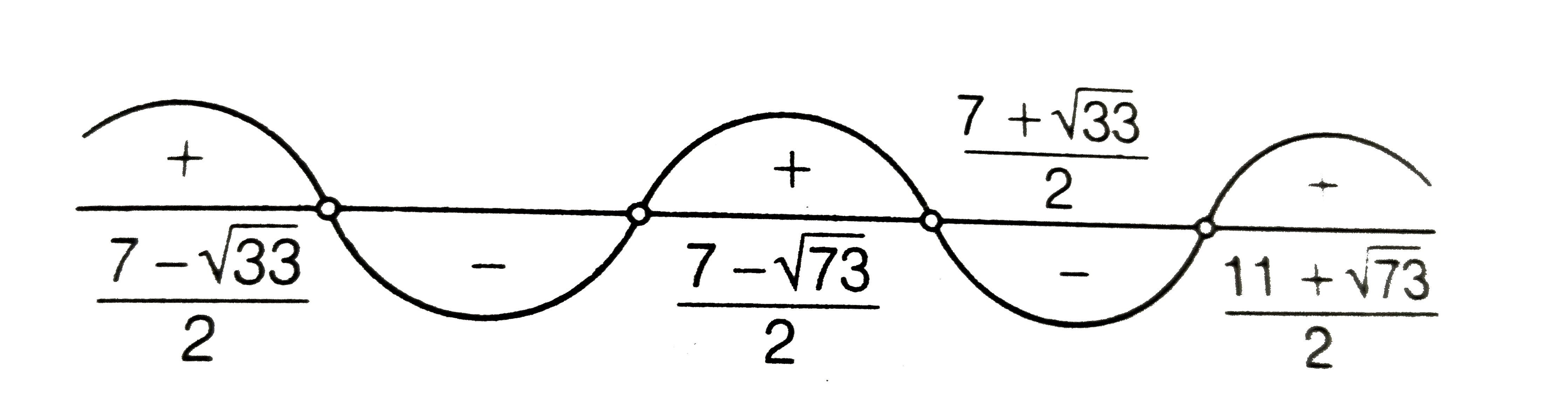
`:. m epsilon ((7-sqrt(33))/2,(11-sqrt(33))/2)uu((7+sqrt(33))/2,(11+sqrt(73))/2)`
Combining all cases we get
`m epsilon `((7-sqrt(33))/2,(11-sqrt(73))/2))uu((7+sqrt(33))/2,(11+sqrt(73))/2)`
(v) One root is smaller than 1 and the other root is greater than 1.
Consiser the following cases.
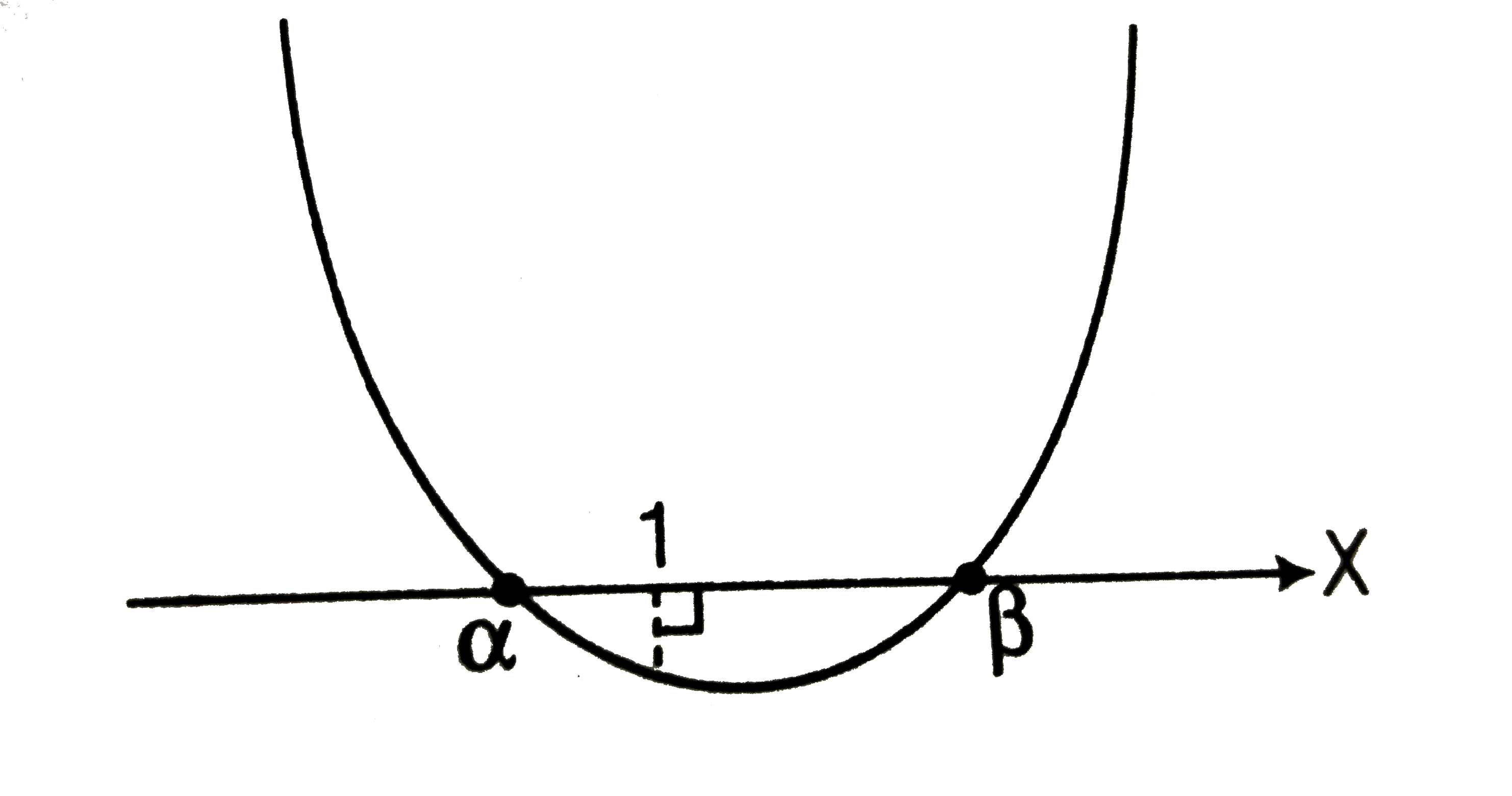
Case I `Dgt0`
`:.m epsilonR` [from Eq. (i)]
Case II `f(1)lt0`
`implies1-(2+1)+1/2m(m+1)lt0` [from Eq. (iii) ]
`impliesm^(2)-3mlt0`
`impliesm(m-3)lt0`
`:.m epsilon (0,3)`
Combining both cases we get
` m epsilon(0,3)`
(vi) One root is greater than 3 and the other root is smaller than 2. ltbRgt Consiser the following cases
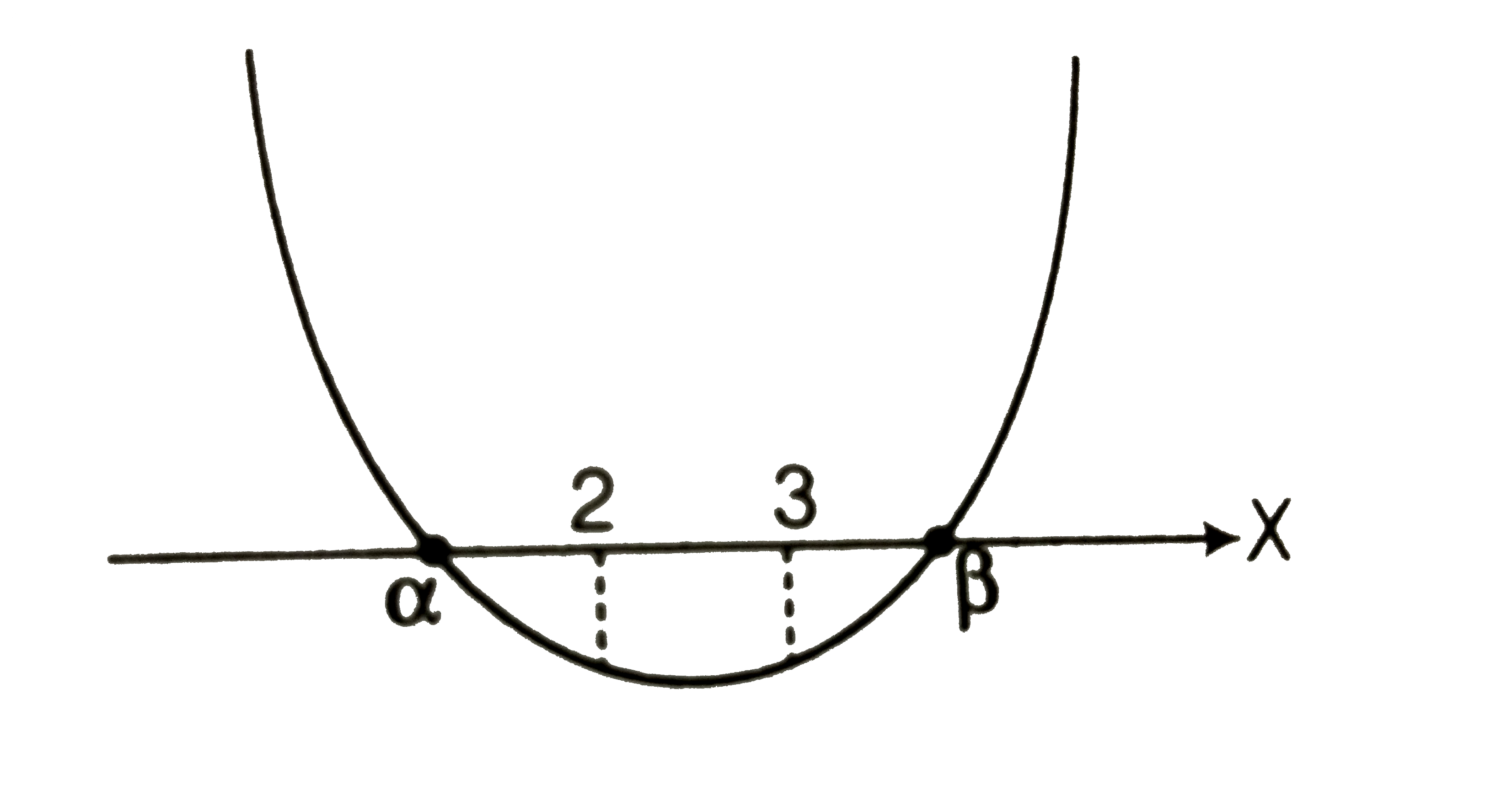
Case I `Dgt0`
`:. m epsion R` [from Eq. (i) ]
Case II `f(2)lt0`
`impliesm^(2)-8m+4lt0`
`:.(7-sqrt(33))/2ltmlt(7+sqrt(33))/2`
`:. m epsilon ((7-sqrt(33))/2ltm lt (7+sqrt(33))/2`
`:. M epsilon ((7-sqrt(33))/2,(7+sqrt(33))/2)`
Case III `f(3)lt0`
`impliesm^(2)-11m+12lt0`
`:.(11-sqrt(73))/2ltmlt (11+sqrt(73))/2`
`:. m epsilon ((11-sqrt(73))/2, (11+sqrt(73))/2)`
Combining all cases we get
`m epsilon ((7-sqrt(33))/2, (7+sqrt(33))/2)`
(vii) Atleast one root lies in the interval (2,3).
i.e. (d) `uu` (c)
`:.mepsilon((7-sqrt(33))/2,(11-sqrt(73))/2)uu((7+sqrt(33))/2,(11+sqrt(73))/2)`
(viii) At least one root is greater than 2.
i.e (Exactly one root is greater than 2) `uu` (Both roots are greater 2).
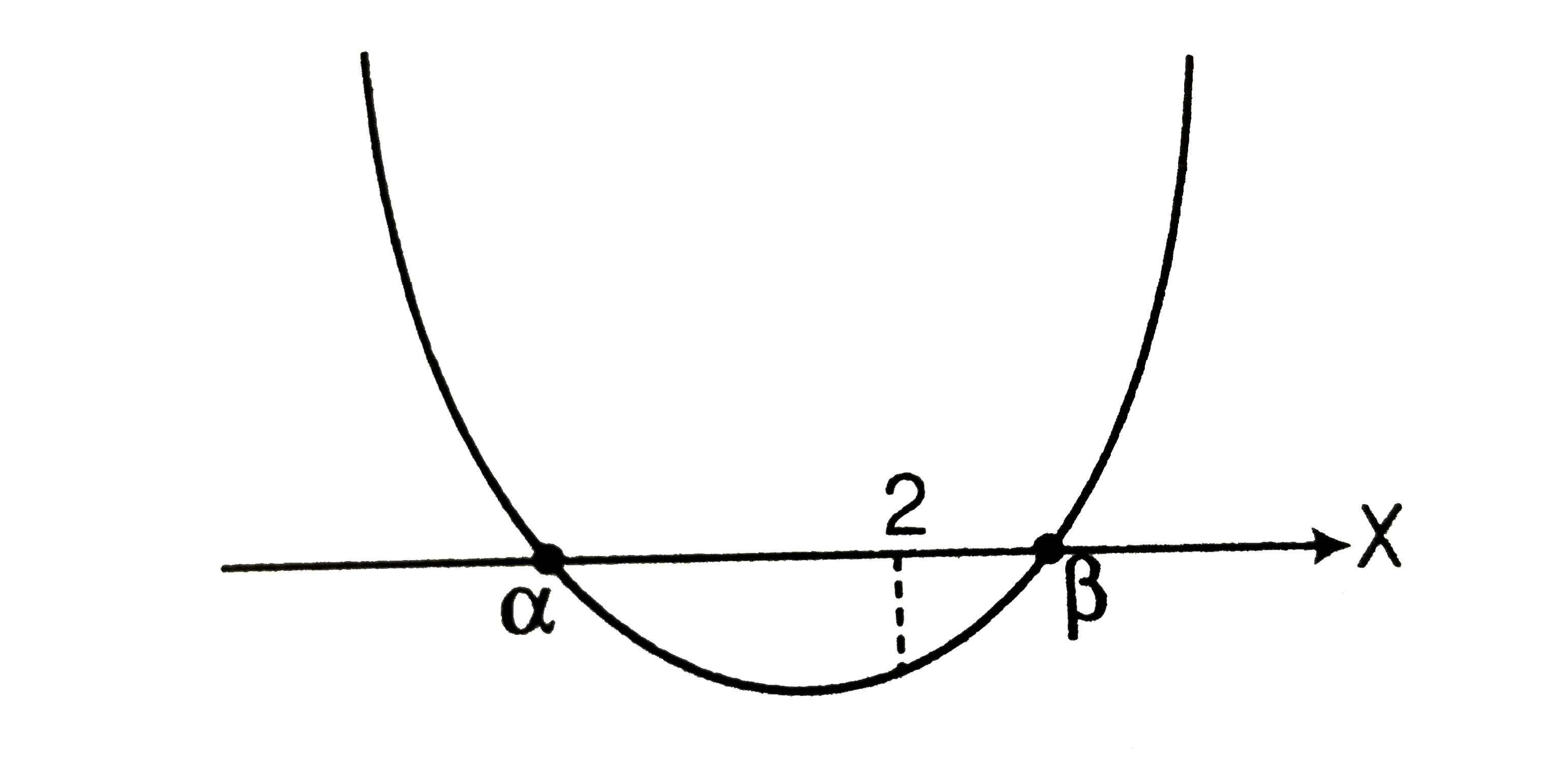
of (Exactly one root is greater than 2) `uu` (b)…..i
Consider the following cases:
Case I `Dgt0`
`:. m epsilon`[from Eq. (i)]
Case II `f(2)lt0`
`impliesm^(2)-7m+4lt0`
`:.m epsilon ((7-sqrt(33))/2,(7+sqrt(33))/2)`
Combining both cases we get
`m epsilon ((7-sqrt(33))/2,(7+sqrt(33))/2)`………ii
Finally from Eqs i and ii we get
` m epsilon ((7-sqrt(33))/2,(7+sqrt(33))/2)uu((7+sqrt(33))/2,oo)`
(ix) Atleast one root is smaller than 2.
i.e (Exactly one root is smaller then 2) `uu` (Both roots are smaller than2)
or (h) II `uu`(a)
We get `m epsilon (-oo,(7-sqrt(33))/2)uu((7-sqrt(33))/2,(7+sqrt(33))/2)`
(x) Both 2 and 3 lie between `alpha` and `beta`
Consider the following cases:
Case `Dgt0`
`:. mepsilonR` [from Eq (i)]
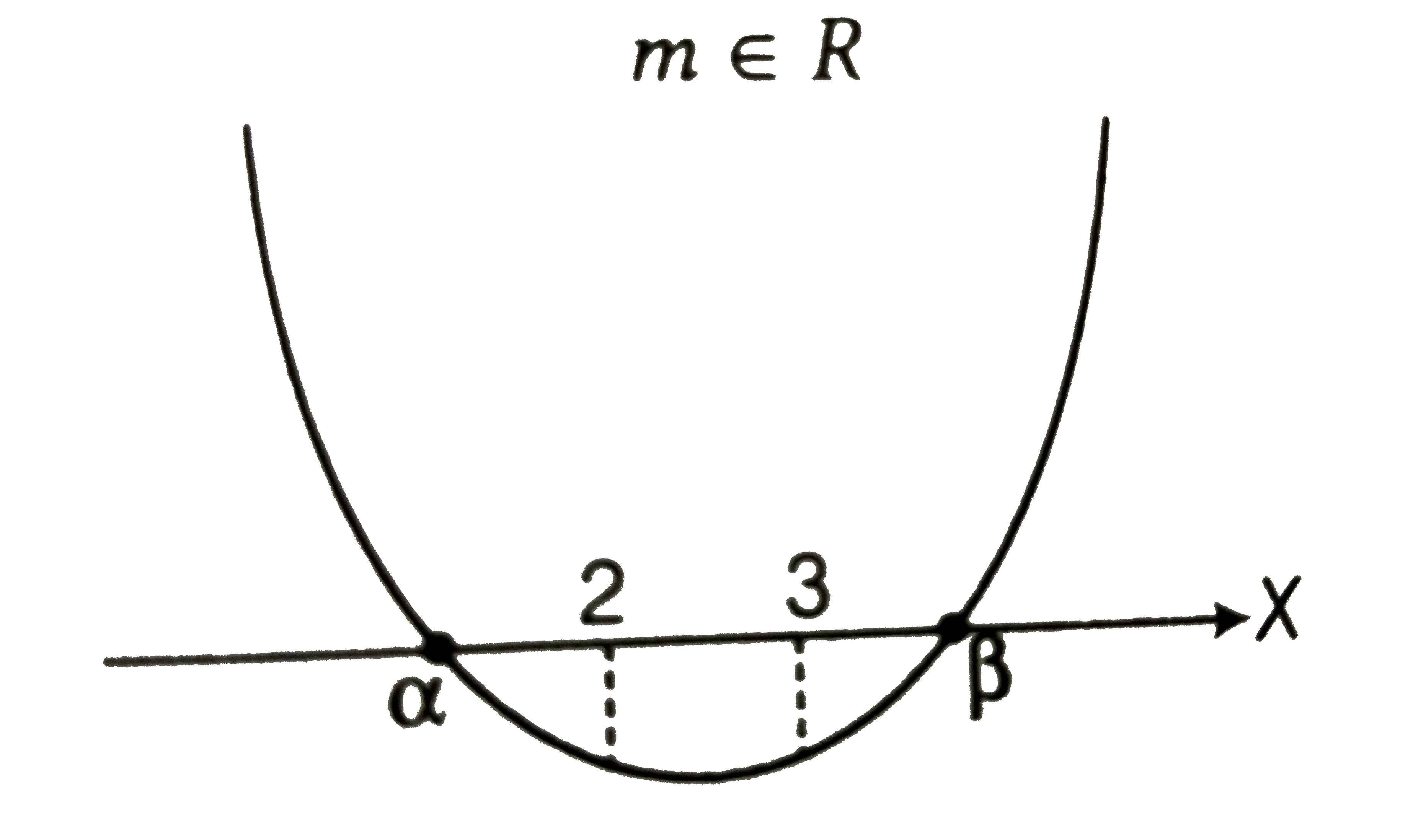
Case II `f(2)lt0`
`impliesm^(2)-7m+4lt0`
`:. m epsilon ((7-sqrt(33))/2,(7+sqrt(33))/2)`
Case III `f(3)lt0`
`impliesm^(2)-11m+12lt0`
`:.m epsilon((11-sqrt(73))/2,(11+sqrt(73))/2)`
Combining all cases we get
`m epsilon ((11-sqrt(73))/2,(7+sqrt(33))/2)`
`:.D=[-2(2m+1)]^(2)-8m(m+1)[D=b^(2)-4ac]`
`=4{(2m+1)^(2)-2m(m+1)}`
`=4(2m^(2)+2m+1)`
`=8(m^(2)+m+1/2)=8{(m+1/2)^(2)+1/4}gt0`
or `D gt0, AA m epsiolonR`……i
x coordinate of vertex `=-b/(2a)=(2(m+1))/4=(m+1/2)`.....ii
and let
`f(x)=x^(2)-(2m+1)x+1/2m(m+1)` ...........iii
(i) Both roots are smaller than 2.

Consider the following cases:
Case I `Dge0`
`:. m epsilonR` [from Eq. (i) ]
CaseII x-coordinate of vertex `lt2`.
`impliesm+1/2lt0` [from Eq. (ii) ]
or `mlt3/2`
Case III `f(2)gt0`
`implies4-(2m+1)2+1/2m(m+1)gt0`
`impliesm^(2)-7m+4gt0`
`:.m epsilon(-oo,(7-sqrt(3))/2)uu((7+sqrt(33))/2,oo)`
Combining all cases we get
`m epsilon (-oo,(7-sqrt(3))/2)`
(ii) Both roots are greater than 2.
Consider the following cases.

Case I `Dge0`
`:. m epsilon R`[from Eq. (i)]
Case II x- coordinate of vertex `gt2`
`impliesm+1/2gt2`[ from Eq. (ii)]
`:.m gt3/2`
Case III `f(2)gt0`
`m epsilon (-oo,(7-sqrt(33))/2)uu(7+(sqrt(33))/2,oo)` [from part (a) ]
Combining all cases, we get
`m epsilon ((7+sqrt(33))/2,oo)`
(iii) Both roots lie in the interval (2,3).
Consider the following cases:

CAse I `Dge0`
`:. m epsilonR` [from Eq. (i)]
Case II `f(2)gt0`
`:. m epsilon (-oo,(7-sqrt(3))/2)uu((7+sqrt(33))/2,oo)` [from part (a)]
Case Case III `f(3)gt0`
`implies9-3(2m+1)+1/2m(m+1)gt0`
or `m^(2)-11m+12gt0`
`:m epsilon (-oo,(11-sqrt(73))/2)uu((11+sqrt(73))/2,oo)`
Case IV `2ltx` -coordinate of vertex `lt3`
`implies2ltm+1/2lt3`
or `3/2ltmlt5/2` or `m epsilon (3/2,5/2)`
Combining allcases we get
`m epsilon phi`
(iv) Exactly one root lie in the interval (2,3).
Consiser the following cases:
Case I `Dgt0`
`:.m epsilon R` [from Eq (i) ]

Case II `f(2)f(3)lt0`
`(4-2(2m+1)+1/2m(m+1))`
`(9-3(2m+1)+1/2m(m+1))lt0`
`implies(m^(2)-7m+4)(m^(2)-11m+12)lt0`
`implies(m-(7-sqrt(33))/2)(m-(7+sqrt(33))/2)`
`(m-(11-sqrt(73))/2)(m-(11+sqrt(73))/2)lt0`
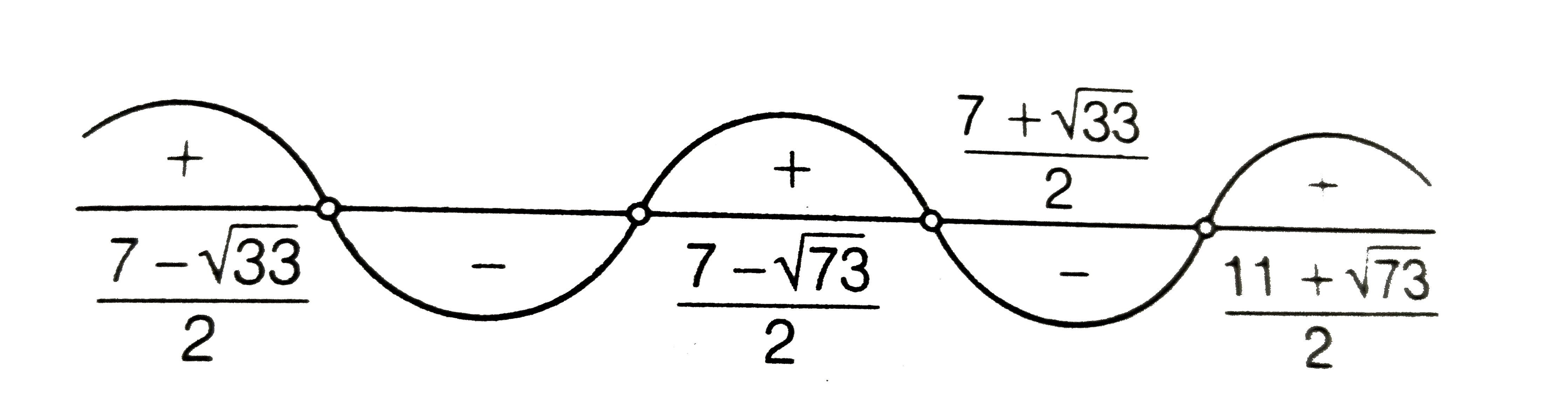
`:. m epsilon ((7-sqrt(33))/2,(11-sqrt(33))/2)uu((7+sqrt(33))/2,(11+sqrt(73))/2)`
Combining all cases we get
`m epsilon `((7-sqrt(33))/2,(11-sqrt(73))/2))uu((7+sqrt(33))/2,(11+sqrt(73))/2)`
(v) One root is smaller than 1 and the other root is greater than 1.
Consiser the following cases.

Case I `Dgt0`
`:.m epsilonR` [from Eq. (i)]
Case II `f(1)lt0`
`implies1-(2+1)+1/2m(m+1)lt0` [from Eq. (iii) ]
`impliesm^(2)-3mlt0`
`impliesm(m-3)lt0`
`:.m epsilon (0,3)`
Combining both cases we get
` m epsilon(0,3)`
(vi) One root is greater than 3 and the other root is smaller than 2. ltbRgt Consiser the following cases

Case I `Dgt0`
`:. m epsion R` [from Eq. (i) ]
Case II `f(2)lt0`
`impliesm^(2)-8m+4lt0`
`:.(7-sqrt(33))/2ltmlt(7+sqrt(33))/2`
`:. m epsilon ((7-sqrt(33))/2ltm lt (7+sqrt(33))/2`
`:. M epsilon ((7-sqrt(33))/2,(7+sqrt(33))/2)`
Case III `f(3)lt0`
`impliesm^(2)-11m+12lt0`
`:.(11-sqrt(73))/2ltmlt (11+sqrt(73))/2`
`:. m epsilon ((11-sqrt(73))/2, (11+sqrt(73))/2)`
Combining all cases we get
`m epsilon ((7-sqrt(33))/2, (7+sqrt(33))/2)`
(vii) Atleast one root lies in the interval (2,3).
i.e. (d) `uu` (c)
`:.mepsilon((7-sqrt(33))/2,(11-sqrt(73))/2)uu((7+sqrt(33))/2,(11+sqrt(73))/2)`
(viii) At least one root is greater than 2.
i.e (Exactly one root is greater than 2) `uu` (Both roots are greater 2).

of (Exactly one root is greater than 2) `uu` (b)…..i
Consider the following cases:
Case I `Dgt0`
`:. m epsilon`[from Eq. (i)]
Case II `f(2)lt0`
`impliesm^(2)-7m+4lt0`
`:.m epsilon ((7-sqrt(33))/2,(7+sqrt(33))/2)`
Combining both cases we get
`m epsilon ((7-sqrt(33))/2,(7+sqrt(33))/2)`………ii
Finally from Eqs i and ii we get
` m epsilon ((7-sqrt(33))/2,(7+sqrt(33))/2)uu((7+sqrt(33))/2,oo)`
(ix) Atleast one root is smaller than 2.
i.e (Exactly one root is smaller then 2) `uu` (Both roots are smaller than2)
or (h) II `uu`(a)
We get `m epsilon (-oo,(7-sqrt(33))/2)uu((7-sqrt(33))/2,(7+sqrt(33))/2)`
(x) Both 2 and 3 lie between `alpha` and `beta`
Consider the following cases:
Case `Dgt0`
`:. mepsilonR` [from Eq (i)]

Case II `f(2)lt0`
`impliesm^(2)-7m+4lt0`
`:. m epsilon ((7-sqrt(33))/2,(7+sqrt(33))/2)`
Case III `f(3)lt0`
`impliesm^(2)-11m+12lt0`
`:.m epsilon((11-sqrt(73))/2,(11+sqrt(73))/2)`
Combining all cases we get
`m epsilon ((11-sqrt(73))/2,(7+sqrt(33))/2)`
Similar Questions
Explore conceptually related problems
Find roots equation 2x^(2)-x-3=0 .
The roots of the equation x^(2)-2sqrt(3)x+3=0 are
Let x^2-(m-3)x+m=0 (m in R) be a quadratic equation . Find the values of m for which the roots are: (ix)one root is smaller than 2 & other root is greater than 2 (x) both the roots are greater than 2. (xi) both the roots are smaller than 2. (xii) exactly one root lies in the interval (1,2) (xiii) both the roots lies in the interval (1,2) (xiv) at least one root lies in the interval (1,2) (xv) one root is greater than 2 and the other root is smaller than 1
Find the values of a for which one root of equation (a-5)x^(2)-2ax+a-4=0 is smaller than 1 and the other greater than 2.
For what values of m the equation (1+m)x^(2)-2(1+3m)x+(1+8m)=0 has (m in R) (i) both roots are imaginary? (ii) both roots are equal? (iii) both roots are real and distinct? (iv) both roots are positive? (v) both roots are negative? (vi) roots are opposite in sign? (vii)roots are equal in magnitude but opposite in sign? (viii) atleast one root is positive? (ix) atleast one root is negative? (x) roots are in the ratio 2:3 ?
If both roots of the equation x^(2)-(m-3)x+m=0(m in R) are positive, then
The number of real roots of the equation |x|^(2) -3|x| + 2 = 0 , is
If the equation (1+m)x^(2)-2(1+3m)x+(1+8m)=0 where m epsilonR~{-1} , has atleast one root negative, then
For what value of m will the equation (x^2-bx)/(ax-c)=(m-1)/(m+1) have roots equal in magnitude but opposite in sign?
All the values of m for whilch both the roots of the equation x^2-2m x+m^2-1=0 are greater than -2 but less than 4 lie in the interval
Recommended Questions
- for what values of m, the equation 2x^(2) -2 ( 2m +1) x+ m ( m +1) = ...
Text Solution
|
- Let x^2-(m-3)x+m=0 (mepsilonR) be a quadratic equation . Find the valu...
Text Solution
|
- Let x^(2) - ( m - 3) x + m = 0 ( m in R) be a quadratic equation. Find...
Text Solution
|
- for what values of m, the equation 2x^(2) -2 ( 2m +1) x+ m ( m +1) ...
Text Solution
|
- All the values of m for which both roots of the equation x^2-2mx +m^2-...
Text Solution
|
- If both the roots of the equation 4x^(2)-2x+m=0 lie in the interval (-...
Text Solution
|
- వేర్ల ద్వారా శాఖీయోత్పత్తి జరిపే మొక్కbr i) డాలియాbr ii) ముల్లంగ...
Text Solution
|
- All the values of m for which both roots of the equation x^(2)-2mx+m^(...
Text Solution
|
- All the values of m for which both roots of the equation x^(2)-2 m x+(...
Text Solution
|