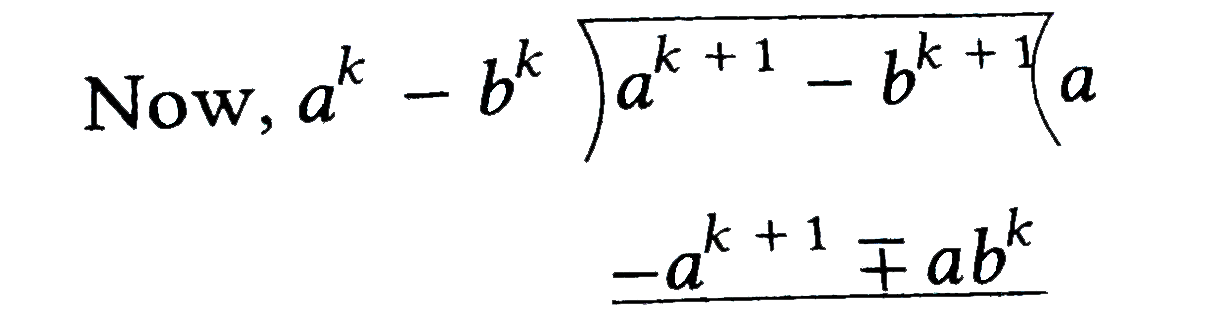Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Use the principle of mathematical induction to show that (a^(n) - b^n)...
Text Solution
|
- Prove the rule of exponents (a b)^n=a^n b^nby using principle of mathe...
Text Solution
|
- Show by using the principle of mathematical induction that for all nat...
Text Solution
|
- Use the principle of mathematical induction to show that 5^(2n+1)+3^(n...
Text Solution
|
- Prove the following by using the Principle of mathematical induction A...
Text Solution
|
- Prove the rule of exponents (ab)^(n) = a^(n)b^(n) by using principle o...
Text Solution
|
- Prove the rule of exponents (ab)^(n) = a^(n)b^(n) by using principle o...
Text Solution
|
- Prove the rule of exponents (ab)^(n) = a^(n)b^(n) by using principle o...
Text Solution
|
- Prove the rule of exponents (a b)^n=a^n b^nby using principle of mathe...
Text Solution
|