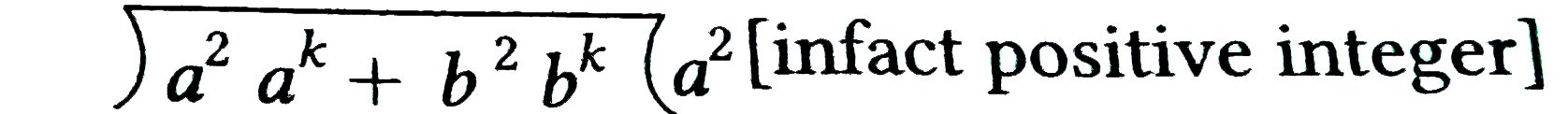Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Prove that the product of three consecutive positive integers is divis...
Text Solution
|
- Prove that one of every three consecutive positive integers is divi...
Text Solution
|
- Prove that one of every three consecutive positive integers is divisib...
Text Solution
|
- Prove that the product of two consecutive positive integers is divi...
Text Solution
|
- Statement-1: The smallest positive integer n such that n! can be expre...
Text Solution
|
- सिद्ध कीजिए कि प्रत्येक तीन क्रमागत धनात्मक पूर्णांकों में से एक 3 से ...
Text Solution
|
- सिद्ध कीजिए कि दो क्रमागत धनात्मक पूर्णांकों का गुणनफल 2 से भाज्य है।
Text Solution
|
- Prove that the product of two consecutive positive integers is divisib...
Text Solution
|
- The product of r consecutive positive integers is divisible by
Text Solution
|