Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
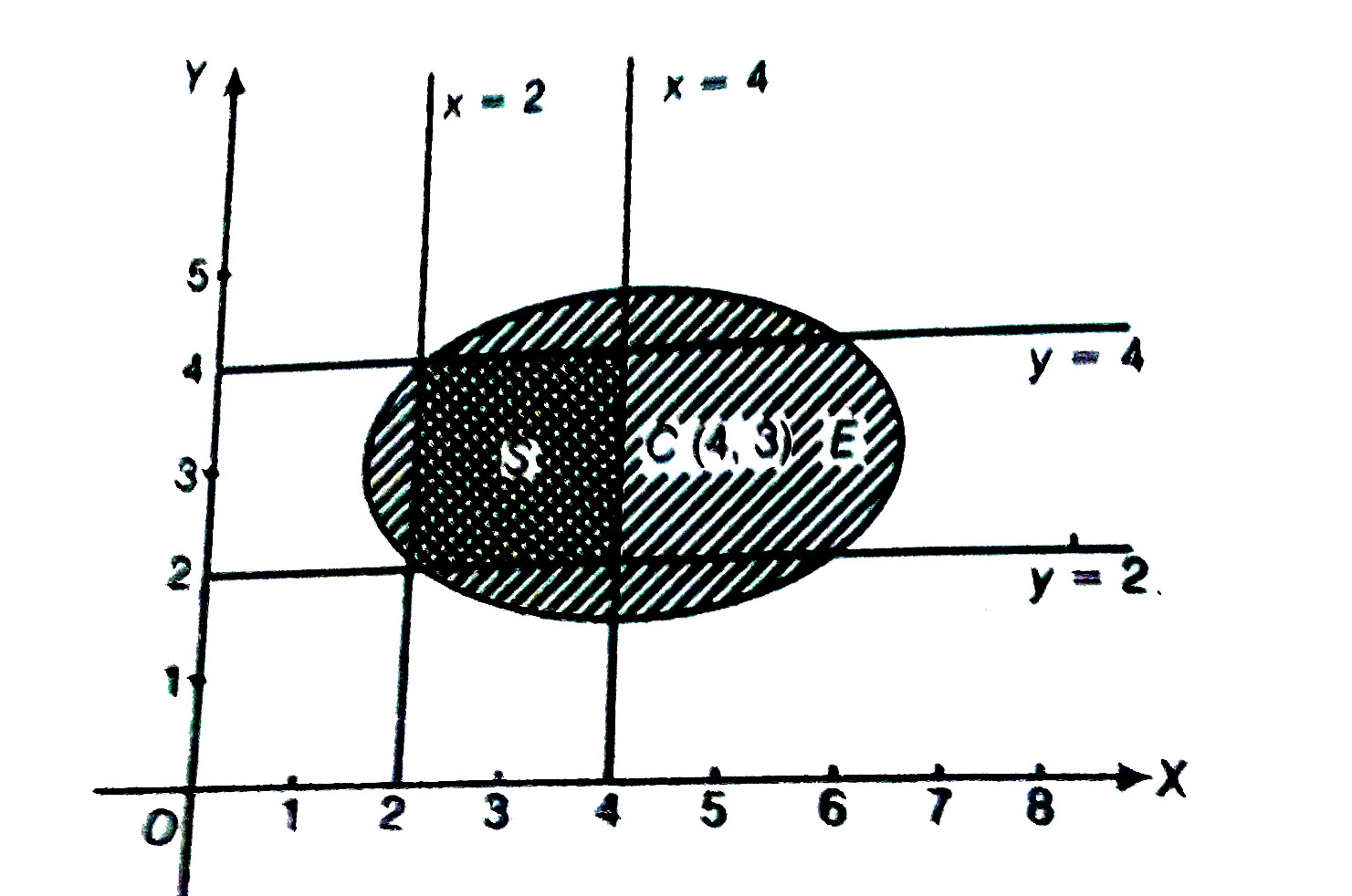
- The sets S and E are defined as given below: S={(x,y): |x-3|lt1and|y...
Text Solution
|
- The sets S and defined as given below S={(x,y):|x|< a and |y| < a},C={...
Text Solution
|
- Indentigy the set of reagents/reacatns conditins (X) and (Y) in the fo...
Text Solution
|
- रूपान्तरण के समुच्चय में अभिकारक समुच्चय /अभिक्रिया परिस्थितियों x और ...
Text Solution
|
- Identify the set of reagents/ reaction condition ‘X’ and ‘Y’ in the fo...
Text Solution
|
- Complete the following reactions : (i) CH(3) - CH(2) Br + KOH "(aque...
Text Solution
|
- In the reaction : CH(3)CH(2)Br underset("Ether")overset(Mg)rarr X unde...
Text Solution
|
- Can Fe^(3+) oxidize Br^(-) " to "Br2 at 1 M concentration ? E^@(Fe^(...
Text Solution
|
- Identify the set of "reagents" // "reaction" conditions 'X' and 'Y' in...
Text Solution
|