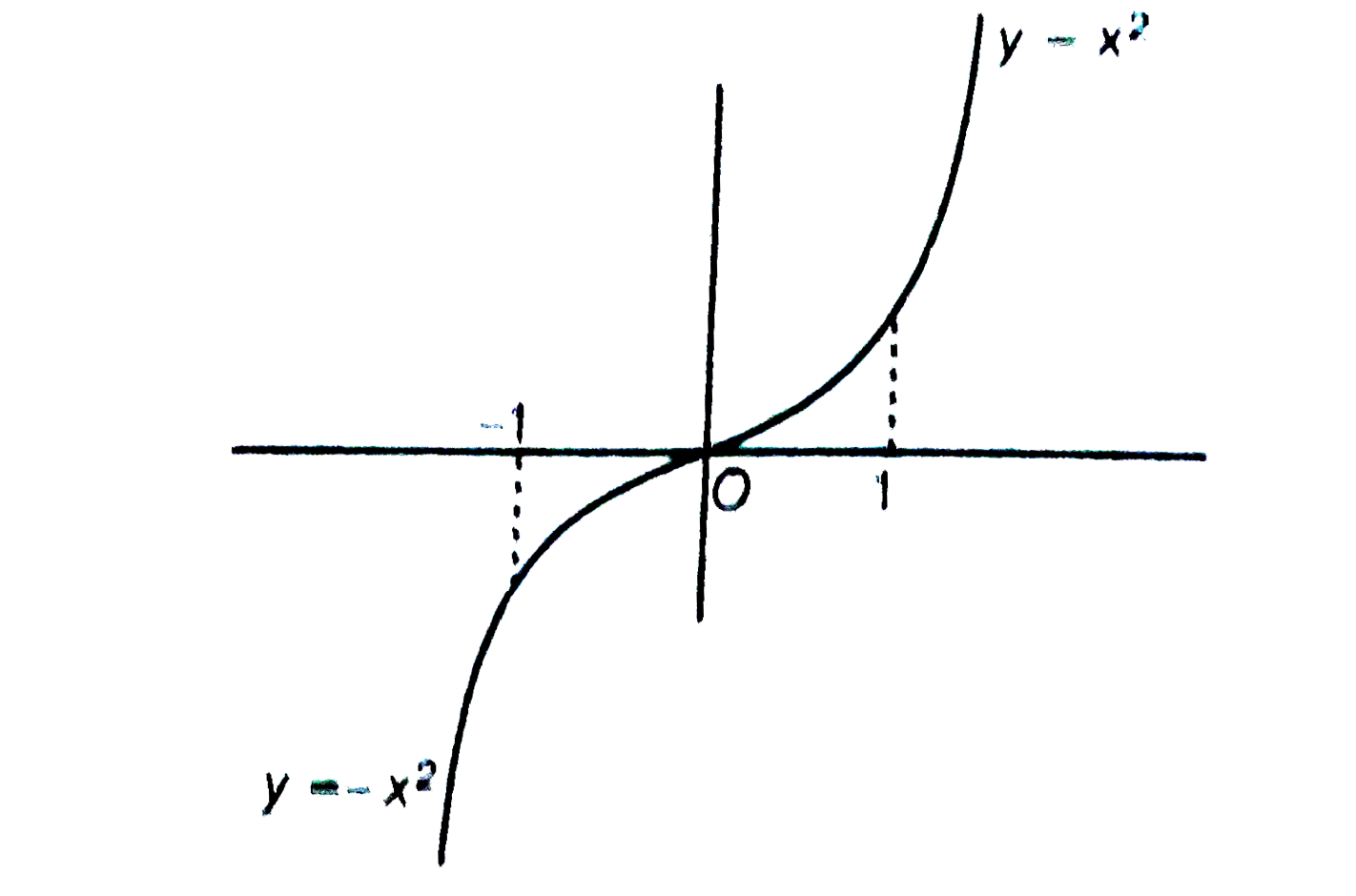
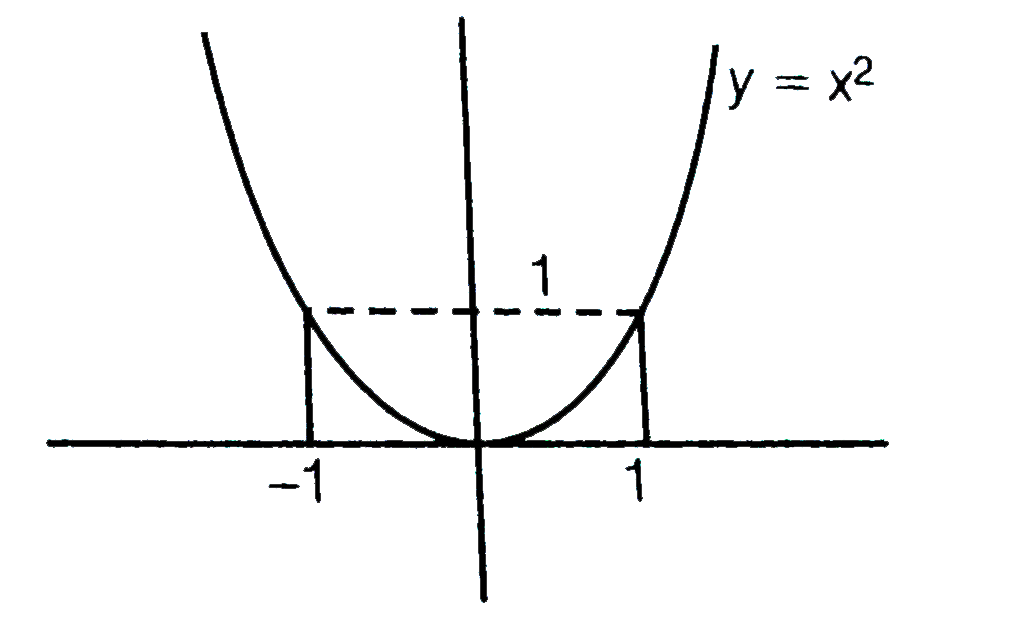
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Let A = {x: -1lexle1} = B for each of the following functions from A t...
Text Solution
|
- Let A=[-1,1]dot Then, discuss whether the following functions from A t...
Text Solution
|
- Let A}x :-1lt=xlt=1}a n df: Avec such that f(x)=x|x|, then f is a bije...
Text Solution
|
- Let A=[-1,\ 1] . Then, discuss whether the following functions from...
Text Solution
|
- Let A={x:-1 le x le 1}=B be a function f: A to B. Then find the nature...
Text Solution
|
- Let RR be the set real numbers and A={x in RR: -1 le x le 1} =B Ex...
Text Solution
|
- Write the coefficient of x ^(2) in each of the following br> (i) 15 - ...
Text Solution
|
- Write the coefficient of x ^(2) in each of the following br> (i) 15 - ...
Text Solution
|
- Write the coefficient of x ^(2) in each of the following br> (i) 15 - ...
Text Solution
|