Home
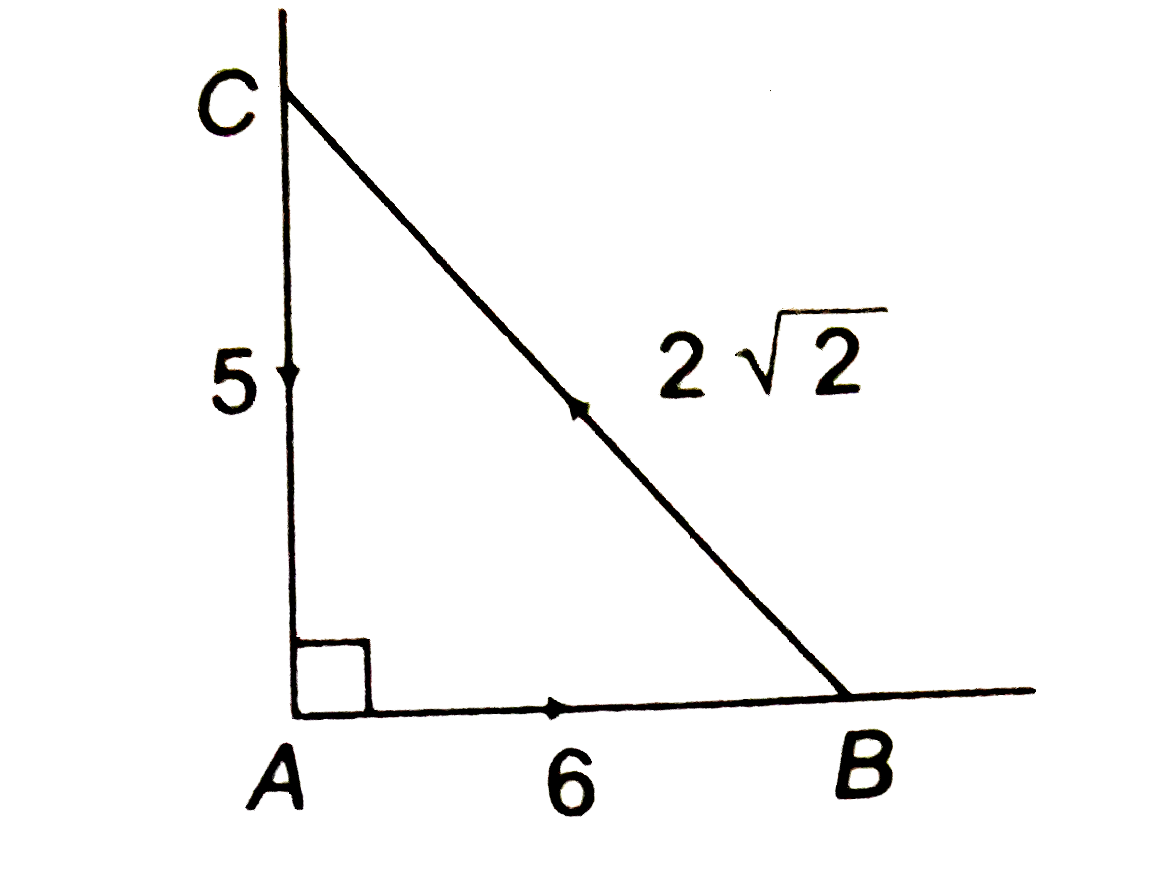
Class 12
MATHS
ABC is an isosceles triangle right angle...

ABC is an isosceles triangle right angled at A. forces of magnitude `2sqrt(2),5 and 6` act along BC, CA and AB respectively. The magnitude of their resultant force is

A

4

B

5

C

`11+2sqrt(2)`

D

30

Text Solution

Verified by Experts

The correct Answer is:
B
R `costheta=6cos0^(@)+2sqrt(2)cos(180^(@)-B)+5sin270^(@)`
`Rcostheta=6-2sqrt(2)cosB` . . (i)
`Rsintheta=6sin0^(@)+2sqrt(2)sin(180^(@)-B)+5sin270^(@)`

`Rsintheta=2sqrt(2)sinB-5` . . . (ii)
From Eqs. (i) and (ii), we get
`R^(2)=36+8cos^(2)B-24sqrt(2)cosB+8sin^(2)B+25-20sqrt(2)sinB`
`=61+8(cos^(2)B+sin^(2)B)-24sqrt(2)cosB-20sqrt(2)sinB`
`because` ABC is a right angled isosceles triangle.
i.e., `angleB=angleC=45^(@)`
`thereforeR^(2)=61+8(1)-24sqrt(2)(1)/(sqrt(2))-20sqrt(2)*(1)/(sqrt(2))=25`
`thereforeR=5`.
Promotional Banner

Similar Questions

Explore conceptually related problems

ABC is an isosceles triangle, right angled at C. Prove that AB^(2)= 2AC^(2) .

ABC is an isosceles triangle right angled at C. Prove that AB^(2) = 2AC^(2) .

The magnitudes of mutually perpendicular forces a,b and c are 2,10 and 11 respectively. Then the magnitude of its resultant is

Two forces of magnitudes 3N and 4N are acted on a body. The ratio of magnitude of minimum and maximum resultant force on the body is

ABC is an isosceles triangle right angled at B. Similar triangles ACD and ABE are constructed on sides AC and AB. Find the ratio between the areas of Delta ABE and Delta ACD

ABC is an isosceles triangle with AB = AC. Draw AP bot BC to show that angle B = angle C

ABC is a right triangle right angled at B. Let D and E be any points on AB and BC respectively. Prove that AE^(2) + CD^(2) = AC^(2) + DE^(2) .

A triangle ABC right angled at A has points A and B as (2, 3) and (0, -1) respectively. If BC = 5 units, then the point C is

Three ant P,Q and R are pulling a grain with forces of magnitude 6N,3sqrt(3) N " and " 3sqrt(2)N as shown in the figure. Find the magnitude of resultant force (in N ) acting on the grain .

Three forces of magnitudes 2N, 3N and 6N act at corners of a cube along three sides as shown in figure. Find the resultant of these forces in N.