A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
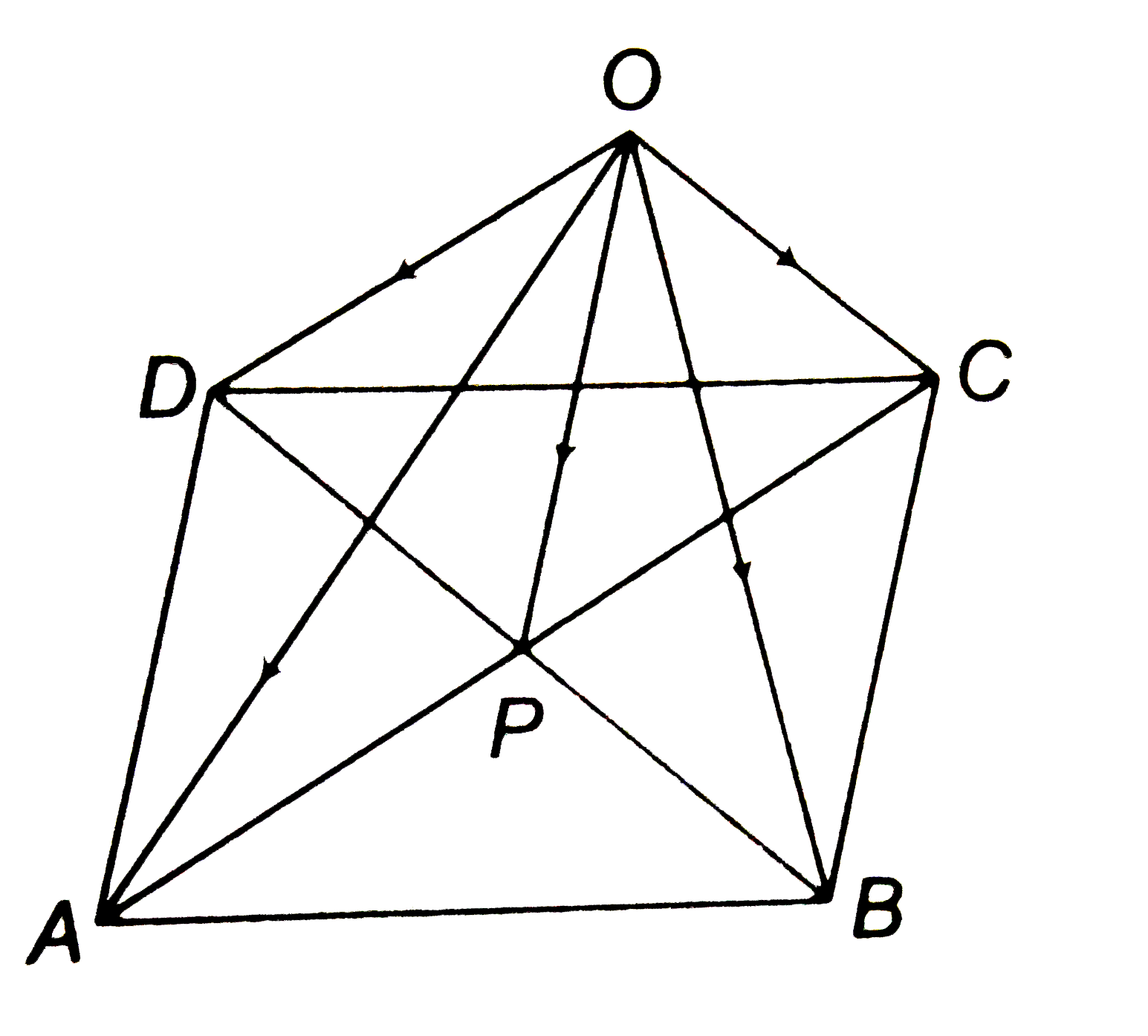
- ABCD is a parallelogram whose diagonals meet at P. If O is a fixed poi...
Text Solution
|
- DeltaABC be an equilateral triangle whose orthocentre is the origin 'O...
Text Solution
|
- DeltaABC be an equilateral triangle whose orthocentre is the origin 'O...
Text Solution
|
- OABCD is a pyramid with square base ABCD such that bar(OA),bar(OB),bar...
Text Solution
|
- ABCD is a parallelogram whose diagonals meet at P. If O is a fixed poi...
Text Solution
|
- If diagonals of a parallelogram ABCD intersect each other in M, then b...
Text Solution
|
- Let G be the centroid of a triangle ABC and O be any other point, then...
Text Solution
|
- Let ABCD be a parallelogram whose diagonals intersect at P and O be th...
Text Solution
|
- ABCD is a quadrilateral and G the point of intersection of the lines j...
Text Solution
|