A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
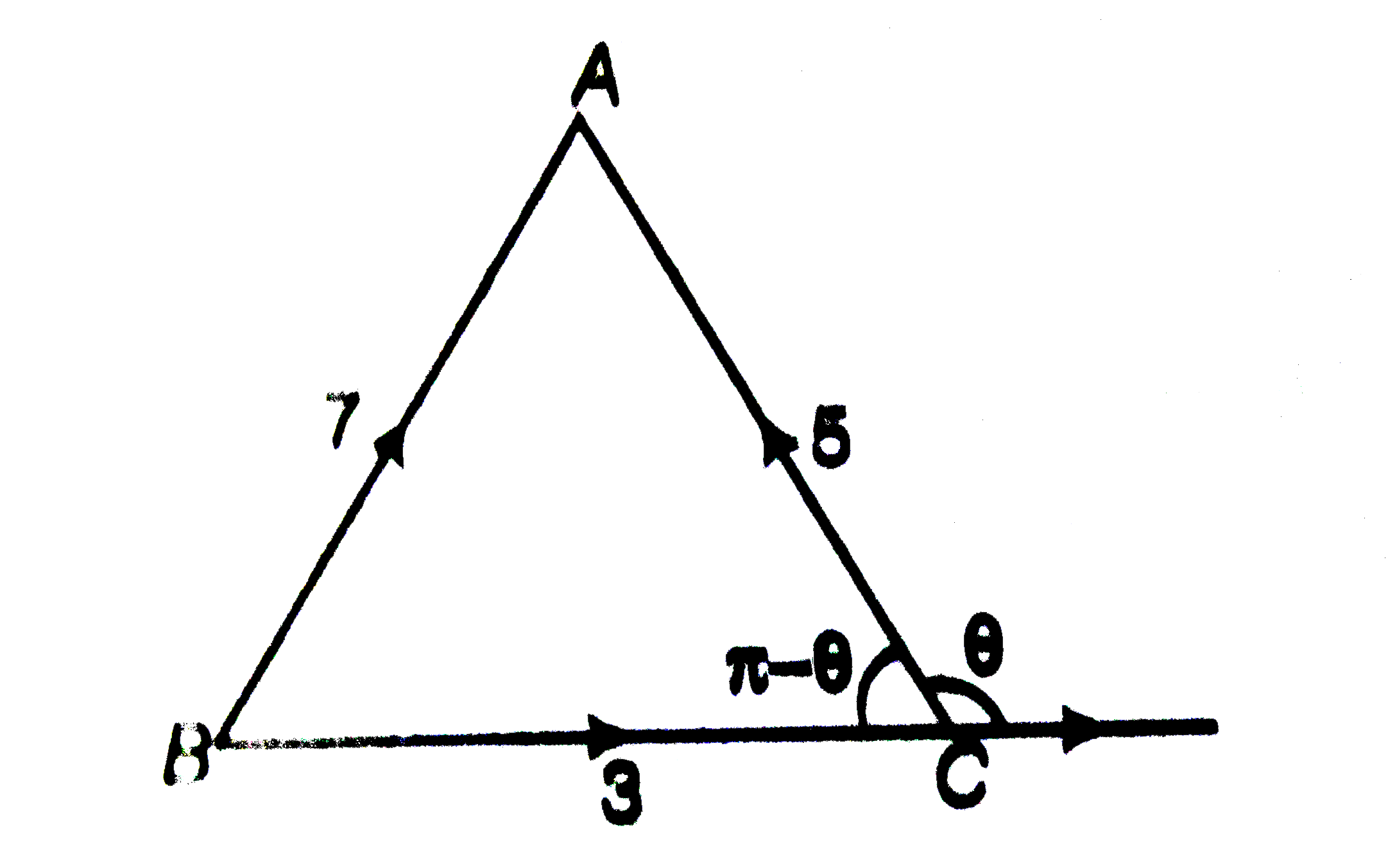
- If veca+vecb+vecc=vec0, |veca| = 3, |vecb| = 5, |vecc| = 7, then angle...
Text Solution
|
- If veca +vecb +vecc=0, |veca|=3,|vecb|=5, |vecc|=7 , then find the ang...
Text Solution
|
- If veca +vecb +vecc =vec0, |veca| =3 , |vecb|=5 and |vecc| =7 , then ...
Text Solution
|
- यदि veca + vecb+ vecc=vec0,|veca|=5,|vecb|=3,|vecc||=7, तो vecaऔर v...
Text Solution
|
- If veca,vecb,vecc are three vectors such that veca+2vecb+vecc=vec0 and...
Text Solution
|
- If veca+vecb+vecc =0, |veca|=3, |vecb|=5, |vecc|=7 then the angle betw...
Text Solution
|
- veca+vecb+vecc=vec0 এবং |veca|=3, |vecb|=5 ও |vecc|=7 হলে veca ও vecbভ...
Text Solution
|
- veca,vecb,vecc எனும் மூன்று வெக்டர்களுக்கு veca+2vecb+vecc=vec0, |veca...
Text Solution
|
- If veca, vecb ,vecc are vectors such that veca + vecb + vecc=0 and |ve...
Text Solution
|