A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
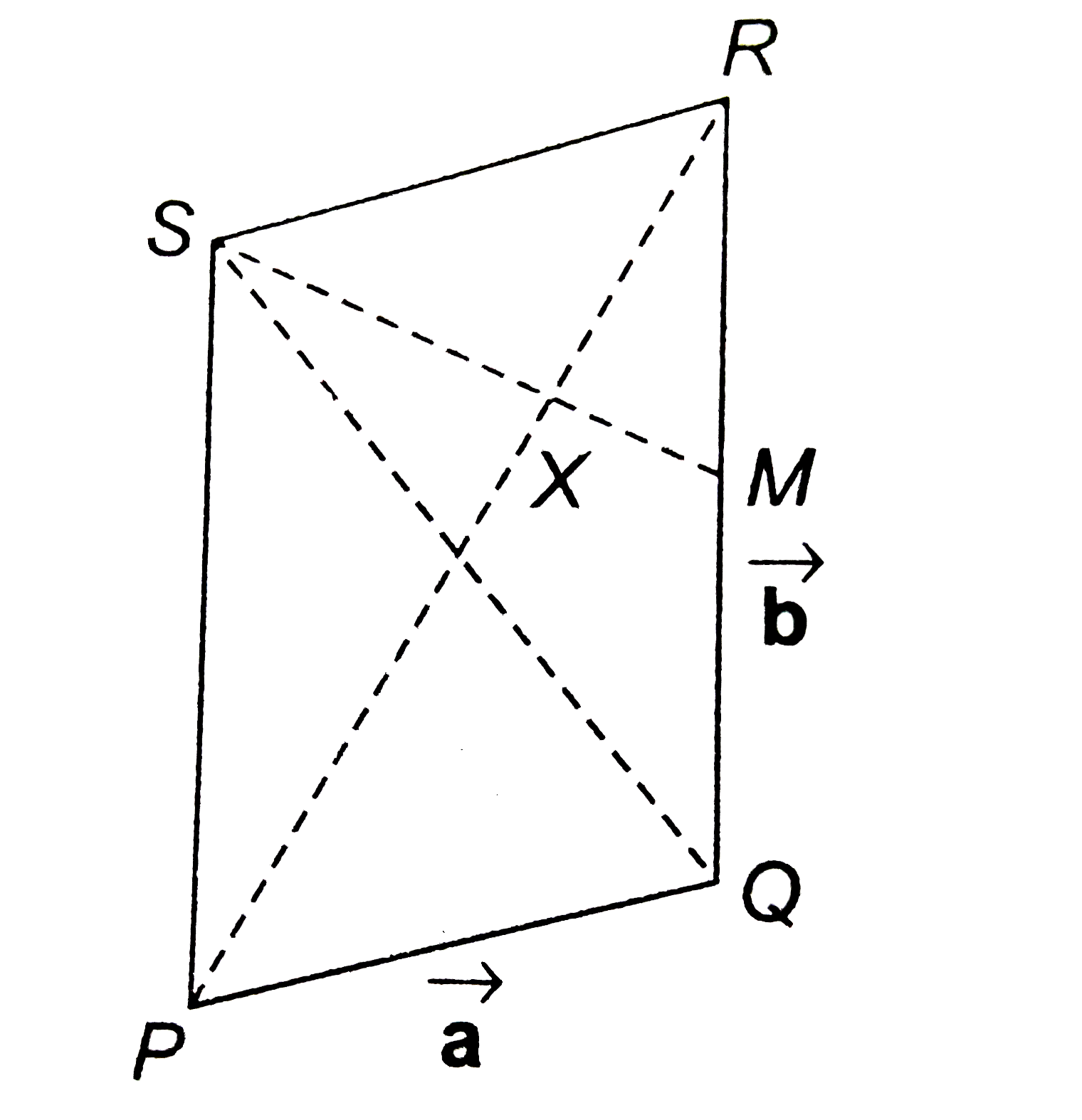
- In a quadrilateral P Q R S , vec P Q= vec a , vec Q R = vec b , vec S ...
Text Solution
|
- Suppose that vec p, vec q and vec r are three non-coplanar vectors in ...
Text Solution
|
- vec p , vec q ,a n d vec r are three mutually perpendicular vectors o...
Text Solution
|
- The projection of point P( vec p) on the plane vec rdot vec n=q is (...
Text Solution
|
- If vec p xxvec q = vec m xxvec n and vec p xxvec m = vec q xxvec n sho...
Text Solution
|
- If vec p=3vec a-5vec b;vec q=2vec a+vec bvec r=vec a+4vec b ; vec s=-v...
Text Solution
|
- If vec p + vec q + vec r = xvec s and vec q + vec r + vec s = yvec p a...
Text Solution
|
- Three vectors vec(P) , vec(Q) and vec( R) are such that |vec(P)| , |ve...
Text Solution
|
- {:("Column- I",,"Column II",),("(Operation of nonzero vectors" vec(P) ...
Text Solution
|