A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
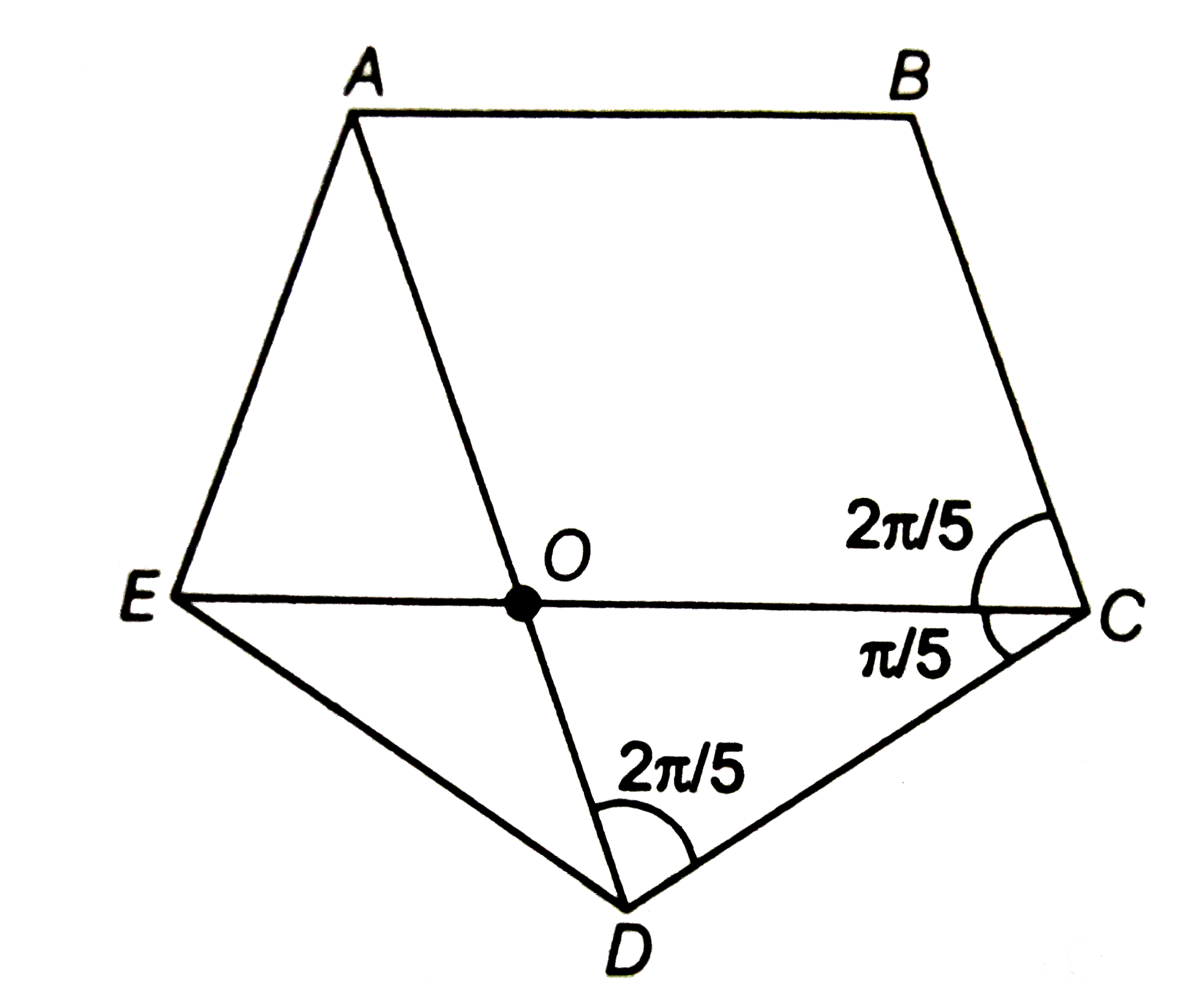
- Let A,B,C,D,E represent vertices of a regular pentangon ABCDE. Given t...
Text Solution
|
- veca,vecb,vecc are the position vectors of vertices A, B, C respective...
Text Solution
|
- ABCD is a parallelogram, and a,b,c and d are the position vector of ve...
Text Solution
|
- Let A, B, C, D, E represent vertices of a regular pentagon ABCDE. Give...
Text Solution
|
- Let A, B, C, D, E represent vertices of a regular pentagon ABCDE. Give...
Text Solution
|
- veca, vecb, vecc समान्तर चतुर्भुज ABCD के क्रमश: शीर्षों A,B,C के स्थि...
Text Solution
|
- A, B, C, D, E, F in that order, are the vertices of a regular hexagon ...
Text Solution
|
- If position vectors of the points A, B and C are a, b and c respectiv...
Text Solution
|
- A, B, C, D, E, F in that order, are the vertices of a regular hexagon ...
Text Solution
|