Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
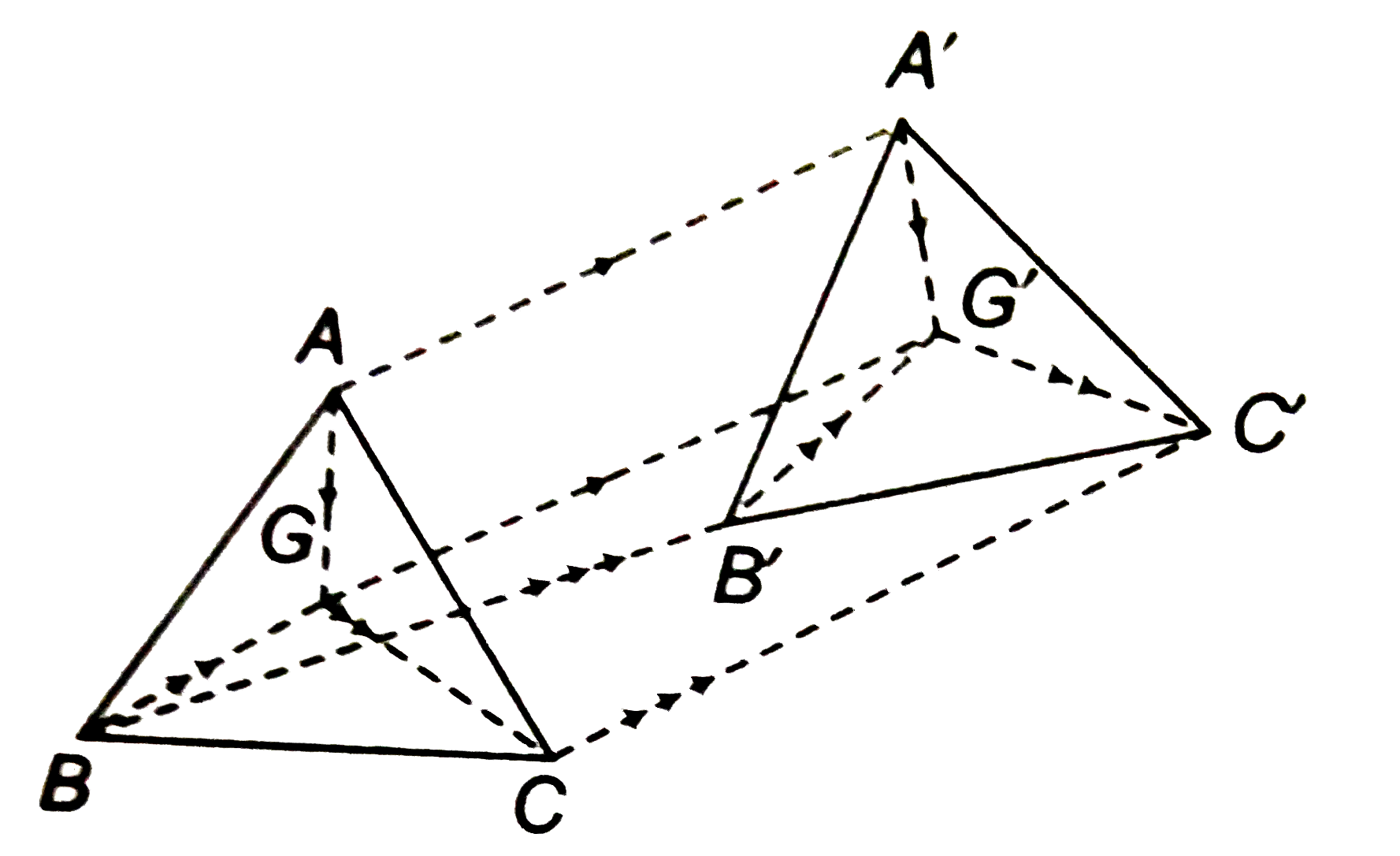
- If G is the centroid of Delta ABC and G' is the centroid of Delta A'...
Text Solution
|
- Let vec(a), vec(b), vec(c) be three vectors in the xyz space such that...
Text Solution
|
- If A, B, C are vertices of a triangle whose position vectors are vec ...
Text Solution
|
- Let G be the centroid of Delta ABC , If vec(AB) = vec a , vec(AC) = v...
Text Solution
|
- यदि त्रिभुज ABC का केन्द्रक G है तब vec(GA)+vec(GB)+vec(GC)=
Text Solution
|
- If G is the centroid of Delta ABC then vec(G)A + vec(G)B + vec(G)C =
Text Solution
|
- If G is the centroid of Delta ABC, G' is the centroid of Delta A' B' C...
Text Solution
|
- If S is the circumcentre, G the centroid, O the orthocentre of Delta A...
Text Solution
|
- G is a point inside the plane of the triangle ABC, if vec(GA)+vec(GB)+...
Text Solution
|