Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
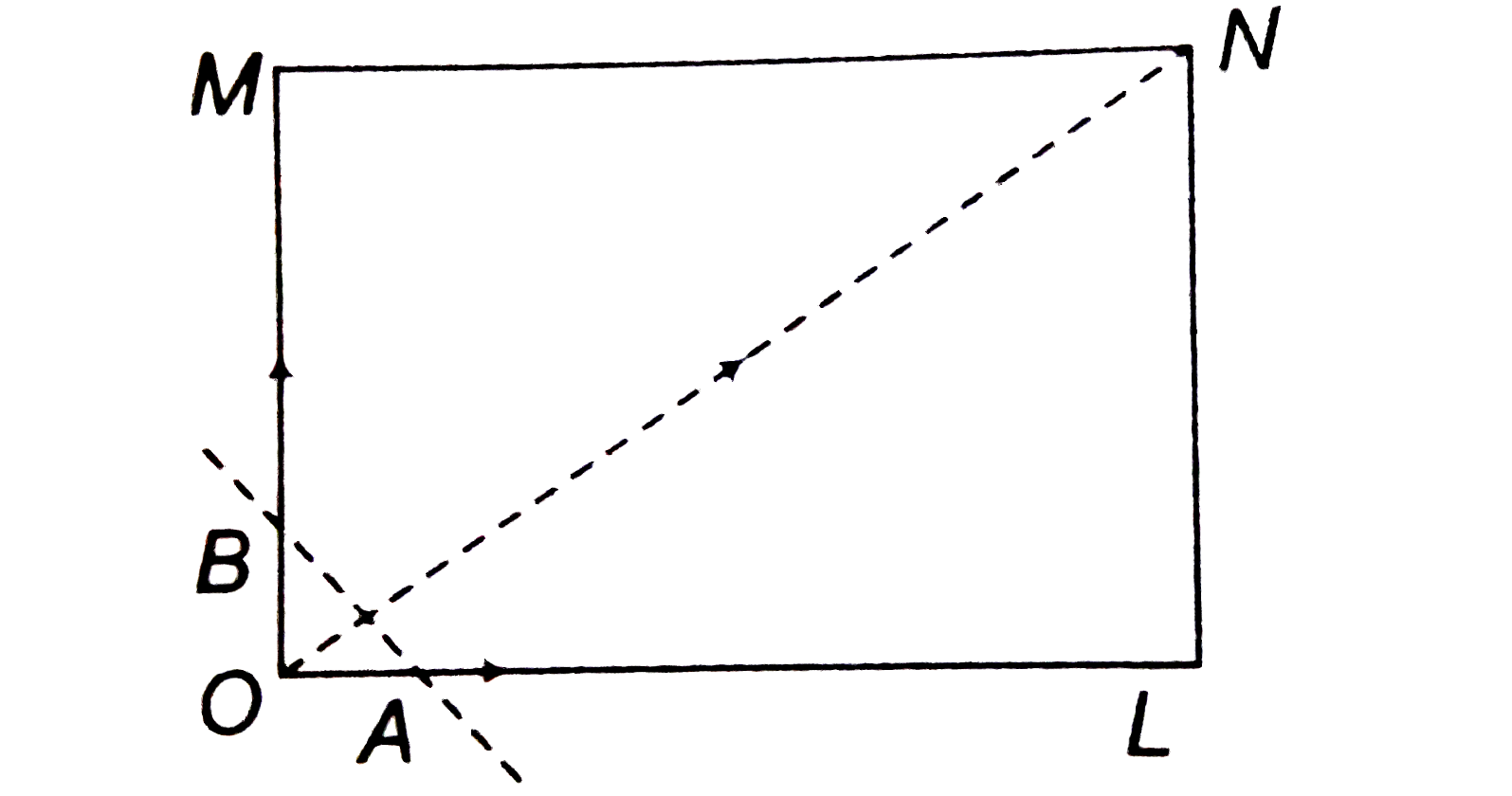
- Statement -1 : If a transversal cuts the sides OL, OM and diagonal O...
Text Solution
|
- Let vec a , vec b , vec c be the position vectors of three distinct p...
Text Solution
|
- Three points with position vectors vec(a), vec(b), vec(c ) will be co...
Text Solution
|
- Statement -1 : If veca and vecb are non- collinear vectors, then point...
Text Solution
|
- veca , vec b , vec c are non-coplanar vectors and x vec a + y vec b ...
Text Solution
|
- ABCD समान्तर चतुर्भुज के विकर्ण P पर मिलते है O कोई बिंदु है। सिद्ध क...
Text Solution
|
- ABCD एक समान्तर चतुर्भुज के विकर्ण P पर मिलते है, O कोई बिन्दु है। सिद...
Text Solution
|
- दिखाए गए वेक्टरो vec(OA), vec(OB) तथा vec(OC) के परिमाण बराबर है। वेक्...
Text Solution
|
- तीन वेक्टर vec(OA), vec(OB) तथा vec(OC) दिखाए गए है। वृत्त कि त्रिज्या...
Text Solution
|