A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
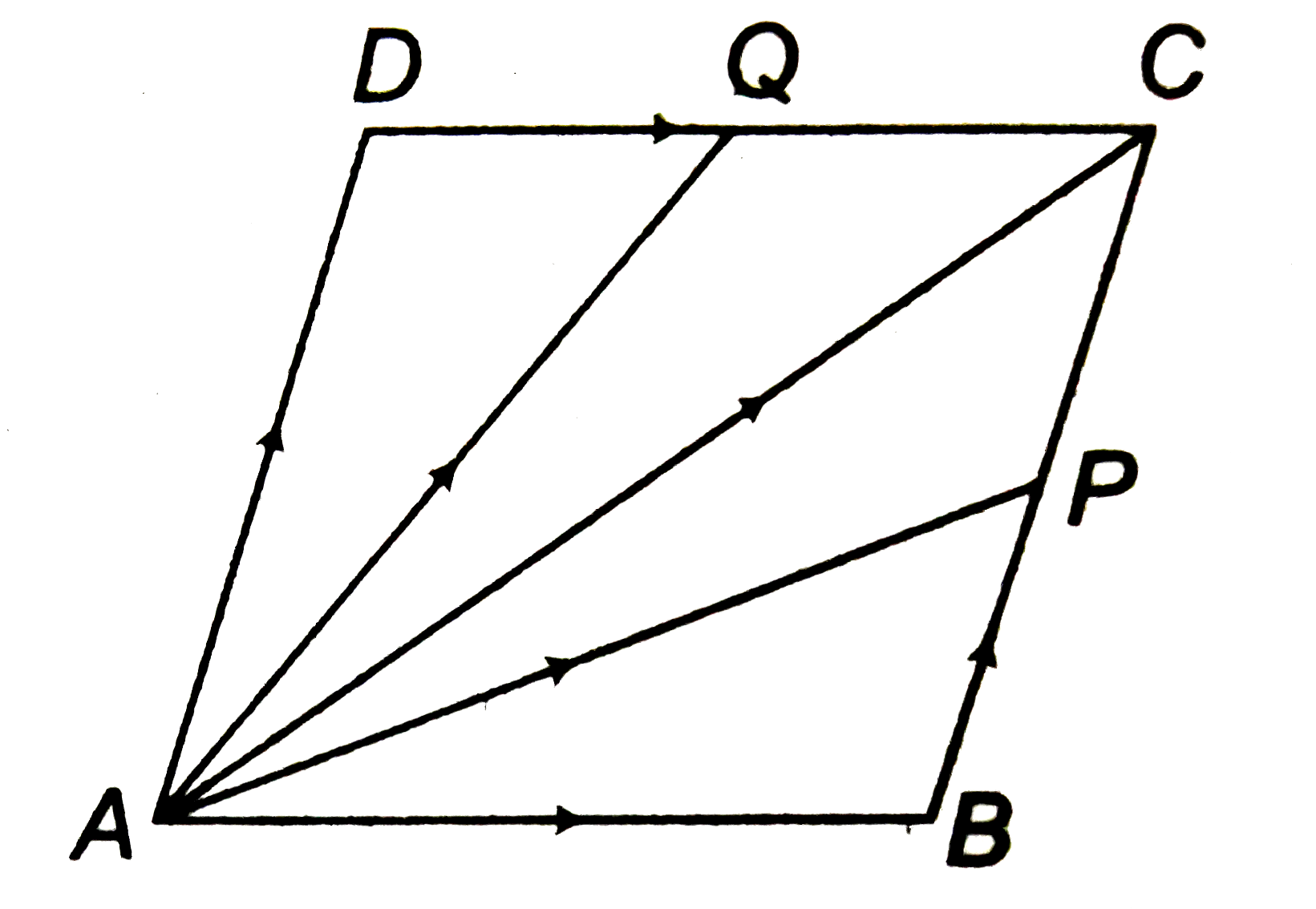
- If P and Q are the middle points of the sides BC and CD of the paralle...
Text Solution
|
- A B C D is a quadrilateral; P , Q , Ra n dS are the points of trisecti...
Text Solution
|
- ABCD एक समानान्तर चतुर्भुज है। भुजा BC तथा CD के मध्य बिंदु P तथा Q ह...
Text Solution
|
- ABCD is a parallelogram. Tow points P and Q are taken on sides AD and ...
Text Solution
|
- In parallelogram ABCD,if P, Q are mid-points of BC and CD respectively...
Text Solution
|
- If M and N are the mid - points of the sides BC and CD respectively of...
Text Solution
|
- P, Q, R and S are the mid-point of the sides AB, BC, CD and DA of the ...
Text Solution
|
- एक समान्तर चतुर्भुज ABCD की सम्मुख भुजाओं AB और CD पर क्रमशः बिन्दु P ...
Text Solution
|
- ABCD एक समान्तर चतुर्भुज है। भुजा AD पर बिंदु P इस प्रकार है कि AP ...
Text Solution
|