A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
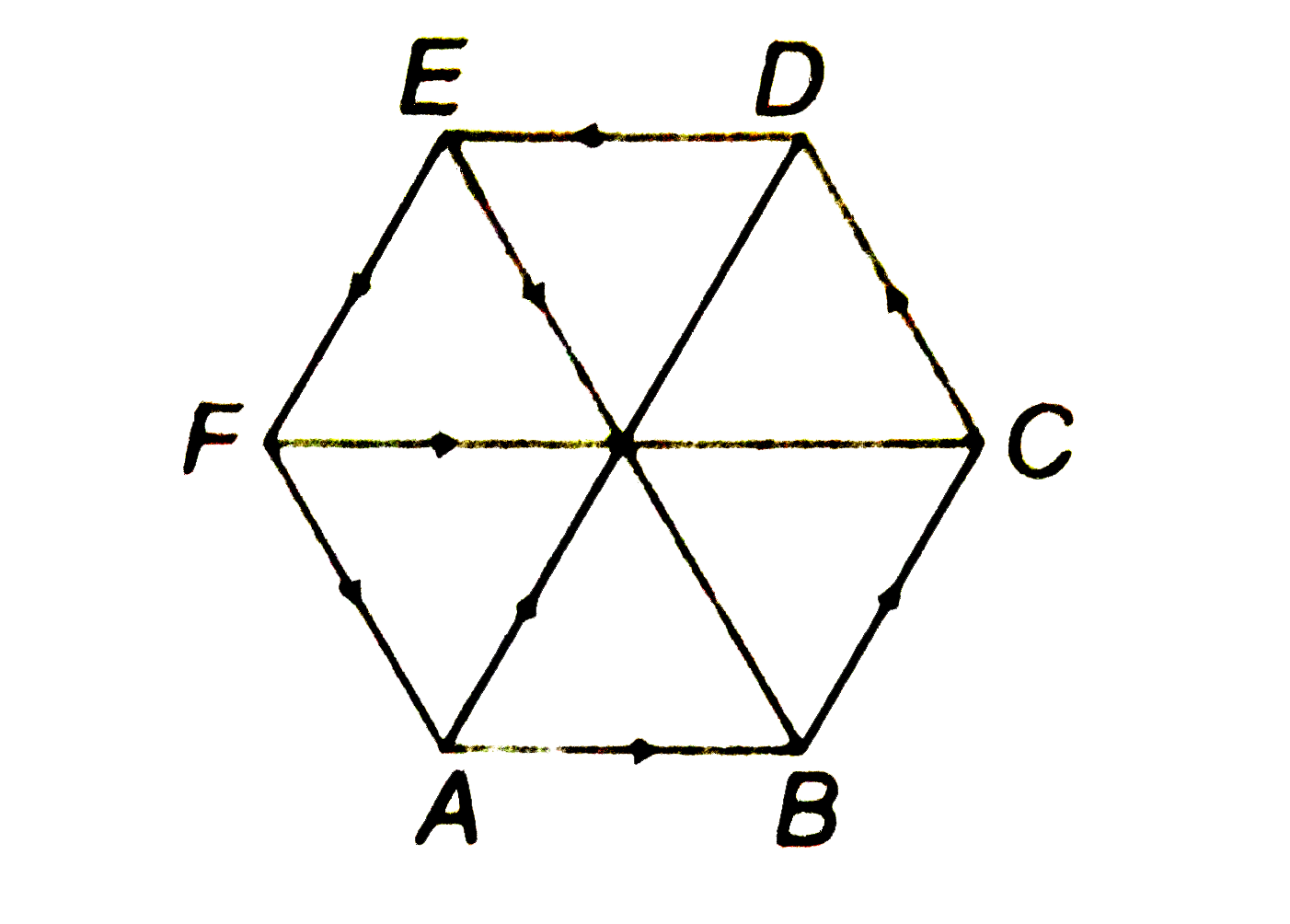
- If ABCDEF is a regular hexagon then vec(AD)+vec(EB)+vec(FC) equals :
Text Solution
|
- If ABCDEF is a regular hexagon with vec AB=vec a and vec BC=vec b, the...
Text Solution
|
- In a regular hexagon ABCDEF, prove that vec(AB)+vec(AC)+vec(AD)+vec(AE...
Text Solution
|
- If ABCDEF is a regular hexagon, prove that vec(AC)+vec(AD)+vec(EA)+vec...
Text Solution
|
- ABCDEF is a regular hexagon with centre a the origin such that vec(AB)...
Text Solution
|
- यदि ABCDEF समपंचभुज हो तो, vec AD +vec EB+vec FC बराबर है-
Text Solution
|
- If ABCDEF be a regular hexagon then (vec(AD)+vec(EB)+vec(FC)) is equa...
Text Solution
|
- If ABCDEF is regular hexagon, then AD+EB+FC is equal to
Text Solution
|
- ABCDEF एक समषटभुज है जिसका केन्द्र O है। यदि vec(AB) + vec(EB) + v...
Text Solution
|