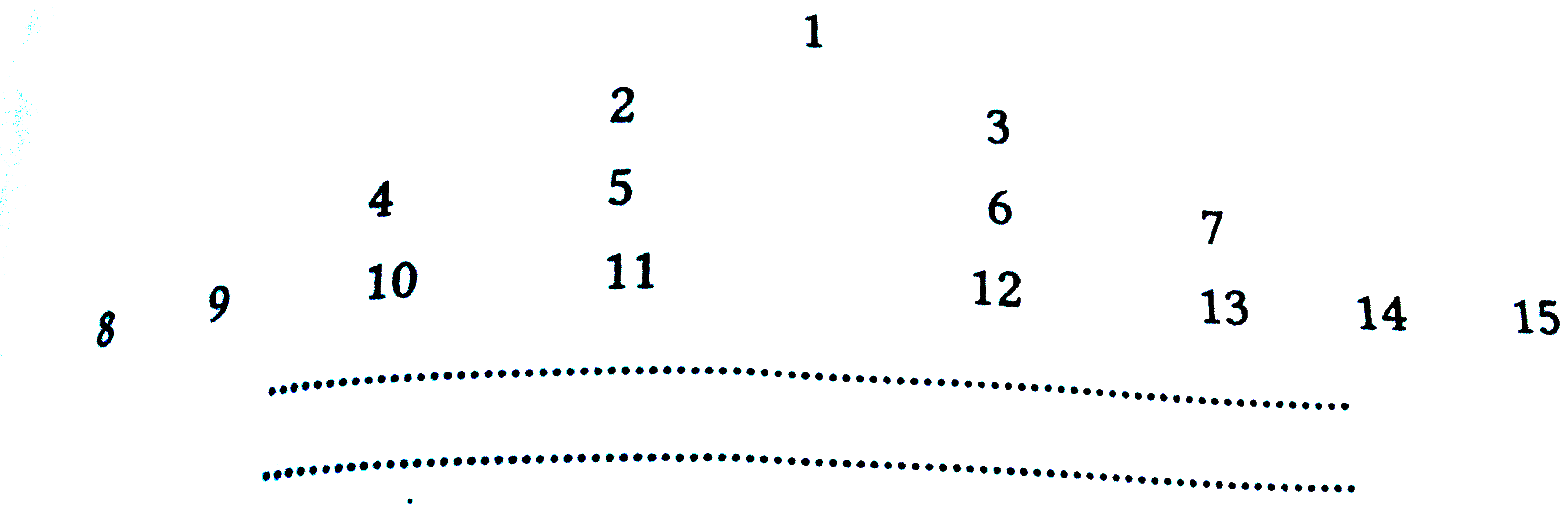Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- The natural numbers arearranged innthe form given below The rth ...
Text Solution
|
- Natural numbers are divided into groups in the following way: 1,(2,3),...
Text Solution
|
- Determine the point of symmetry of a regular hexagon. <img src="htt...
Text Solution
|
- Dtermine the images of the following figure about the given line : ...
Text Solution
|
- Match the following Column A to Column B
Text Solution
|
- Match the following Column A to Column B
Text Solution
|
- Match the following Column A to Column B
Text Solution
|
- Find the area of figure given below.
Text Solution
|
- Find the perimeter of the figure given below.
Text Solution
|