A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
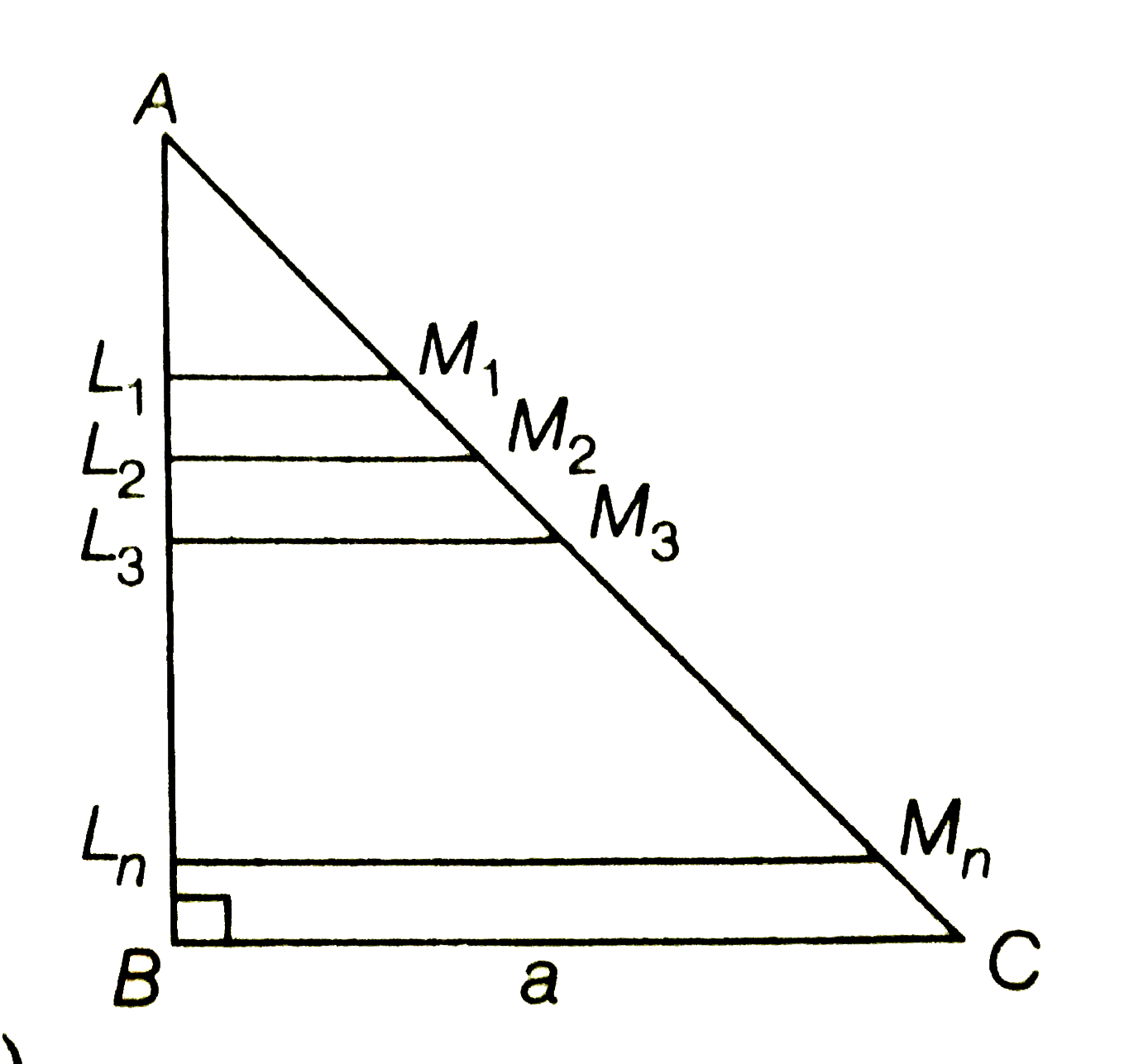
- ABC is a right angled triangle in which /B=90^(@) and BC=a. If n point...
Text Solution
|
- Three sided of a triangle have equations L1-=y-mi x=o; i=1,2a n d3. Th...
Text Solution
|
- ABC is a right-angled triangle in which angleB=90^(@) and BC=a. If n p...
Text Solution
|
- If the direction cosines of two lines are (l(1), m(1), n(1)) and (l(...
Text Solution
|
- ABC is a right angled triangle in which /B=90^(@) and BC=a. If n point...
Text Solution
|
- If (l(1), m(1), n(1)) , (l(2), m(2), n(2)) are D.C's of two lines, th...
Text Solution
|
- यदि (l(1),m(1),n(1)),(l(2),m(2),n(2)) और (l(3),m(3),n(3)) तीन प...
Text Solution
|
- If L(1) = (2.02 +- 0.01)m and L(2) = (1.02 +- 0.01)m then L(1) + 2L(2)...
Text Solution
|
- ABC is a right-angled triangle in which angleB=90^(@) and BC=a. If n p...
Text Solution
|