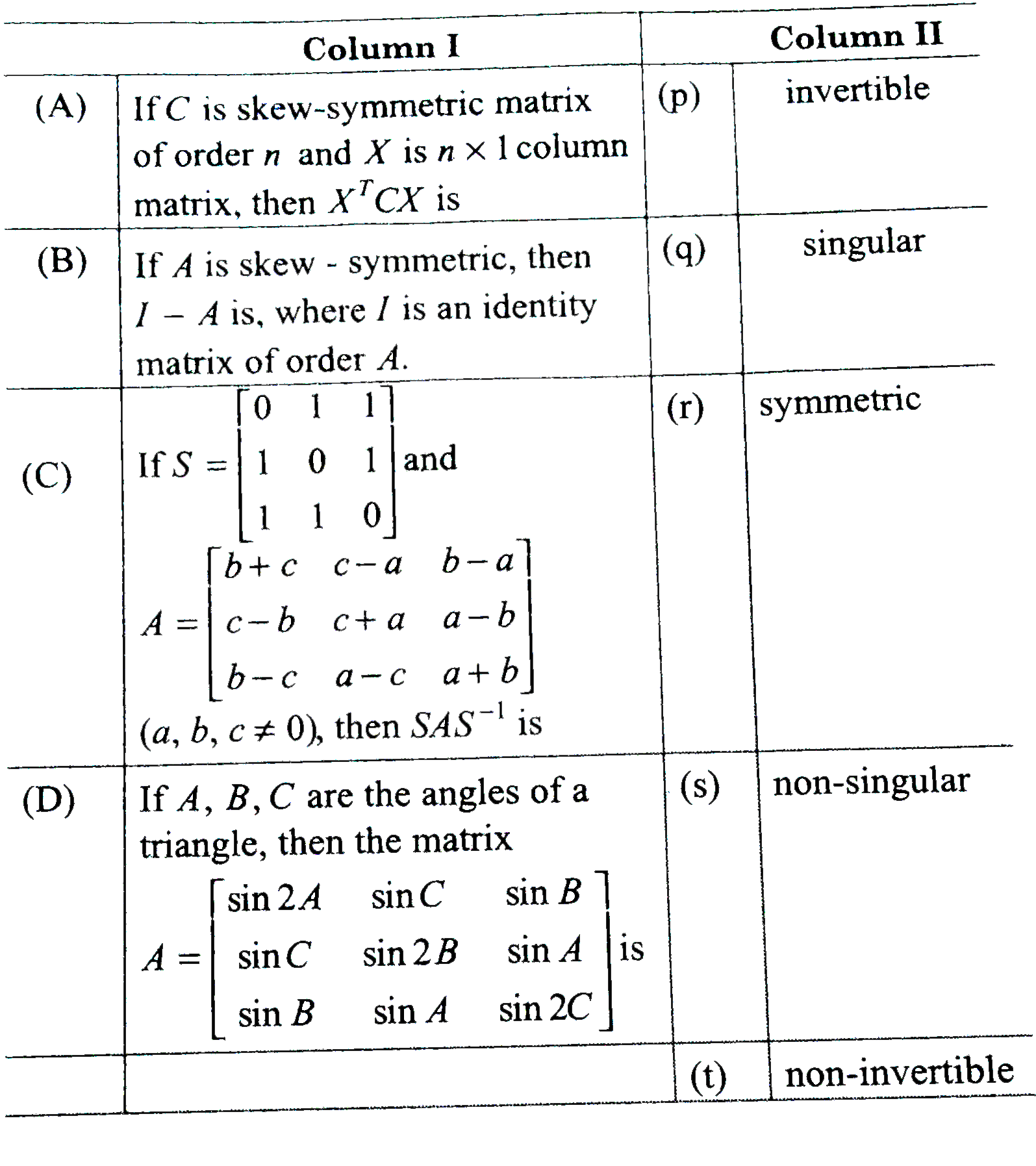`(A) rarr (q,t), (B) rarr (p,s), (C) rarr (p,r,s), (D) rarr (q,r,t)`
(A) Here, X is a n`nxx1` matrix, C is `nxxn` matrix andf `X^(T)` is a
`1xxn` matrix.
Let `X^(T)CX = [lambda]`, then `(X^(T)CX )^(T) = X^(T) C^(T) (X^(T))^(T) = X^(T) (-C)X= - X^(T) CX`
`therefore [lambda] = -[lambda]`
`rArr lambda = 0`
`rArr X^(T )CX = O`
(B) Consider the homogeneous sytemm
`(I-A)X = O`
` rArr AX = IX =X " "...(i)`
Now, `(AX)^(T) = X^(T) A^(T)rArr X^(T) = -X^(T) A`
`rArr X^(T )X = - X^(T) AX = - X^(T) X`
[from Eq. (i) ]
`rArr 2 X^(T) X = O rArr abs(X) = O`
`(I-A) X=O` has only trivial solution
`therefore I - A ` is non- singular
`rArr (I-A)` is invertible
(C) `because S= [[0,1,1],[1,0,1],[1,1,0]]`
`rArr S^(-1) =1/2[[-1,1,1],[1,-1,1],[1,1,-1]]`
We have ` SA= [[0,1,1],[1,0,1],[1,1,0]] [[b+c,c-a,b-a],[c-b,c+a,a-b],[b-c,a-c,a+b]]`
`=[[0, 2a, 2a],[2b, 0, 2b],[2c, 2c, 0]]`
`therefore SAS^(-1)=[[0, 2a, 2a],[2b, 0, 2b],[2c, 2c, 0]]1/2 [[-1,1,1],[1,-1,1],[1,1,-1]]`
`=[[0, a, a],[b, 0, b],[c, c, 0]][[-1,1,1],[1,-1,1],[1,1,-1]][[2a, 0,0],[0,ab,0],[0,0,ac]]`
`abs(SAS^(-1)) = 8abc ne 0 `
`because A = [[sin2A , sinC, sinB],[sinC,sin2B,sinA],[sinB,sinA,sin2C]]`
`abs(A)= [[2akcosA , ck, bk],[ck, 2bk cosB, ak],[bk, ak, 2ck cos C]]`
`= k^(3) [[a cos A+ acos A ,acosB + bcos A , acos C + cos A ],[a cos B + b cos A ,b cosB+ b cos B , b cos C + c cosB ],[a cosC+c cosA,b cosC+c cosB,c cosC+c cosC]]`
`= k^(3) abs( (a, cosA,0),(b,cosB,0),(c , cosC, 0))xxabs((cosA , a, 0 ),(cosB, b, 0),(cosC, c,0))= k^(3) cdot 0cdot0=0`