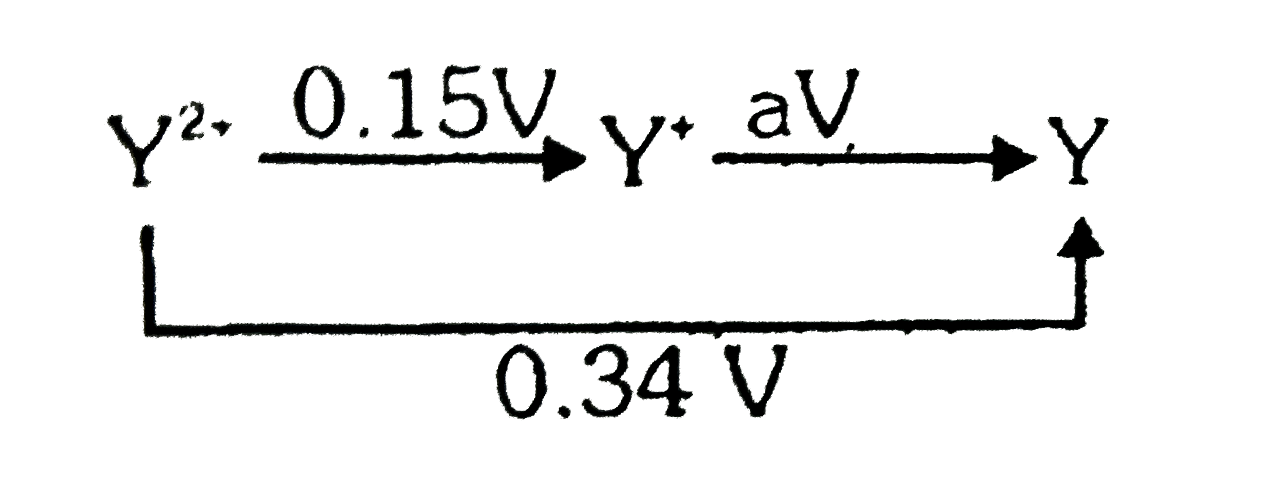A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- The magnitude ( but not the sign ) of the standard reduction potential...
Text Solution
|
- Q.lim(x rarr0,y rarr0)(y^(2)+sin x)/(x^(2)+sin y^(2)), when (x,y)rarr(...
Text Solution
|
- The magnitude ( but not the sign ) of the standard reduction potential...
Text Solution
|
- The magnitude ( but not the sign ) of the standard reduction potential...
Text Solution
|
- When connected to a Standard Hydrogen Electrode (SHE) electrons flow f...
Text Solution
|
- The logarithm of the equilibrium constant of the cell reaction corresp...
Text Solution
|
- Form differential equation for y=e^(x)(a+bx+x^(2)) A)y(2)-2y(1)+y=2e^...
Text Solution
|
- The logarithm of the equilibriium constant of the cell reaction cor...
Text Solution
|
- The standard reduction potentials of metals A and B are x and y respec...
Text Solution
|