Text Solution
Verified by Experts
Topper's Solved these Questions
ELASTICITY, SURFACE TENSION AND FLUID MECHANICS
ALLEN |Exercise Exercise 1 (Elasticity)|16 VideosELASTICITY, SURFACE TENSION AND FLUID MECHANICS
ALLEN |Exercise Exercise 1 (Surface Tension)|21 VideosCENTRE OF MASS
ALLEN |Exercise EXERCISE-V B|19 VideosERROR AND MEASUREMENT
ALLEN |Exercise Part-2(Exercise-2)(B)|22 Videos
Similar Questions
Explore conceptually related problems
ALLEN -ELASTICITY, SURFACE TENSION AND FLUID MECHANICS-Exercise 5 B (Integer Type Questions)
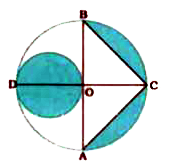
- In the given figure, AB and CD are two diameters of a circle (with cen...
Text Solution
|
- Two soap bubbles A and B are kept in a closed chamber where the air is...
Text Solution
|
- A cylindrical vessel of height 500mm has an orifice (small hole) at it...
Text Solution
|
- Consider two solid spheres P and Q each of density 8gm cm^-3 and diame...
Text Solution
|
_S01_022_S01.png)
_S01_022_S02.png)