Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
ELASTICITY, SURFACE TENSION AND FLUID MECHANICS
ALLEN |Exercise Exercise 4 A (Viscosity)|3 VideosELASTICITY, SURFACE TENSION AND FLUID MECHANICS
ALLEN |Exercise Exercise 4 B (Bran storming Subjective Exercise)|11 VideosELASTICITY, SURFACE TENSION AND FLUID MECHANICS
ALLEN |Exercise Exercise 4 A (Fluid Statics)|13 VideosCENTRE OF MASS
ALLEN |Exercise EXERCISE-V B|19 VideosERROR AND MEASUREMENT
ALLEN |Exercise Part-2(Exercise-2)(B)|22 Videos
Similar Questions
Explore conceptually related problems
ALLEN -ELASTICITY, SURFACE TENSION AND FLUID MECHANICS-Exercise 4 A (Fuild Dynamics)
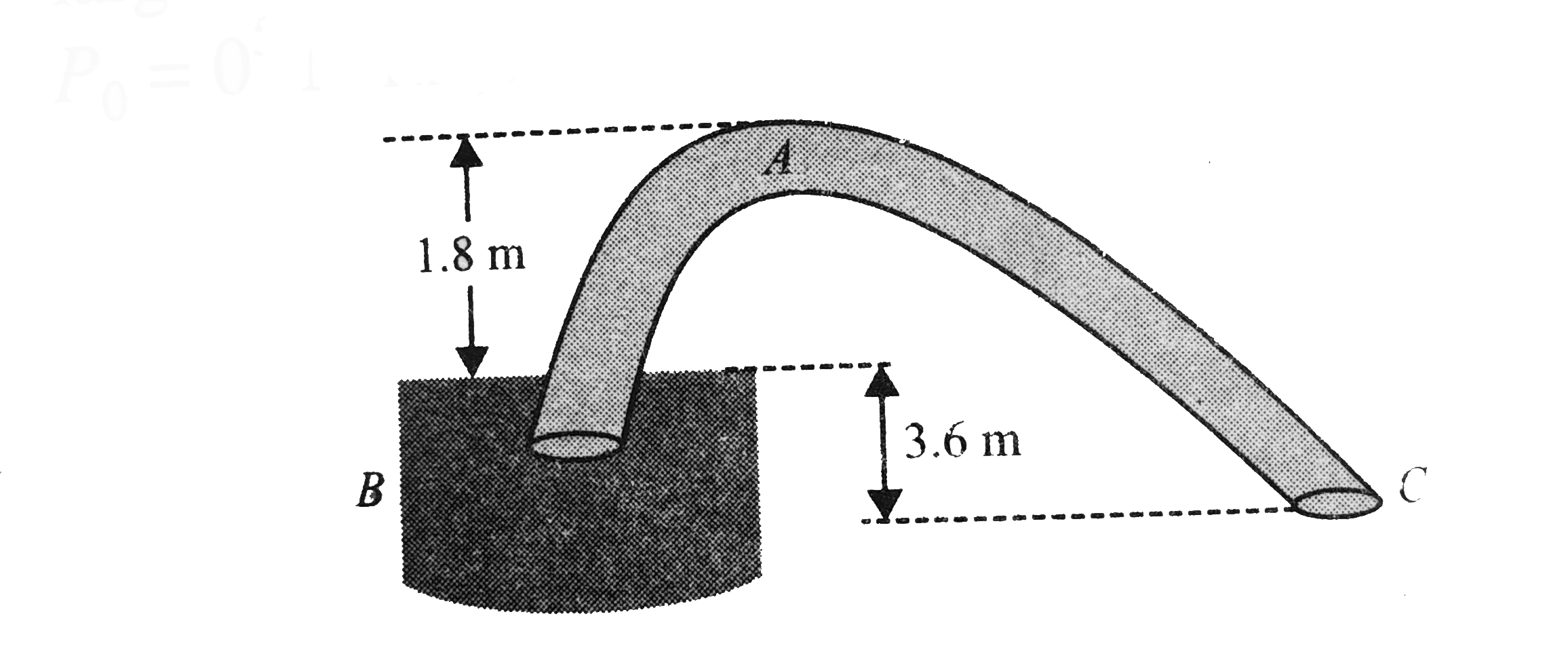
- A non-viscous liquid of constant density 1000kg//m^3 flows in a stream...
Text Solution
|
- A large open top container of negligible mass and uniform cross sectio...
Text Solution
|
- The diagram (figure) shows a venturimeter, through which water is flow...
Text Solution
|
- A siphon has a uniform circular base of diameter 8//sqrt(pi) cm with i...
Text Solution
|
- A syringe containing water is held horizontally with its nozzle at a h...
Text Solution
|
- In a movable container shown in figure a liquid of density rho is fill...
Text Solution
|
- A large tank is filled with two liquids of specific gravities 2sigma a...
Text Solution
|