A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
ELASTICITY, SURFACE TENSION AND FLUID MECHANICS
ALLEN |Exercise Exercise 5 B (Assertion Reason)|1 VideosELASTICITY, SURFACE TENSION AND FLUID MECHANICS
ALLEN |Exercise Exercise 5 B (Subjective Type Questions)|7 VideosELASTICITY, SURFACE TENSION AND FLUID MECHANICS
ALLEN |Exercise Exercise 5 B (Multiple correct answers)|2 VideosCENTRE OF MASS
ALLEN |Exercise EXERCISE-V B|19 VideosERROR AND MEASUREMENT
ALLEN |Exercise Part-2(Exercise-2)(B)|22 Videos
Similar Questions
Explore conceptually related problems
ALLEN -ELASTICITY, SURFACE TENSION AND FLUID MECHANICS-Exercise 5 B (Comprehension)
- A wooden cylinder of diameter 4 r, height H and density rho//3 is kept...
Text Solution
|
- A wooden cylinder of diameter 4 r, height H and density rho//3 is kept...
Text Solution
|
- A wooden cylinder of diameter 4 r, height H and density rho//3 is kept...
Text Solution
|
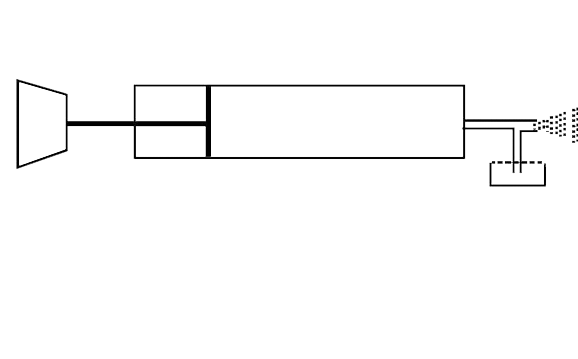
- A spray gun is shown in the figure where a piston pushes air out of a ...
Text Solution
|
- A spray gun is shown in the figure where a piston pushes air out of a ...
Text Solution
|