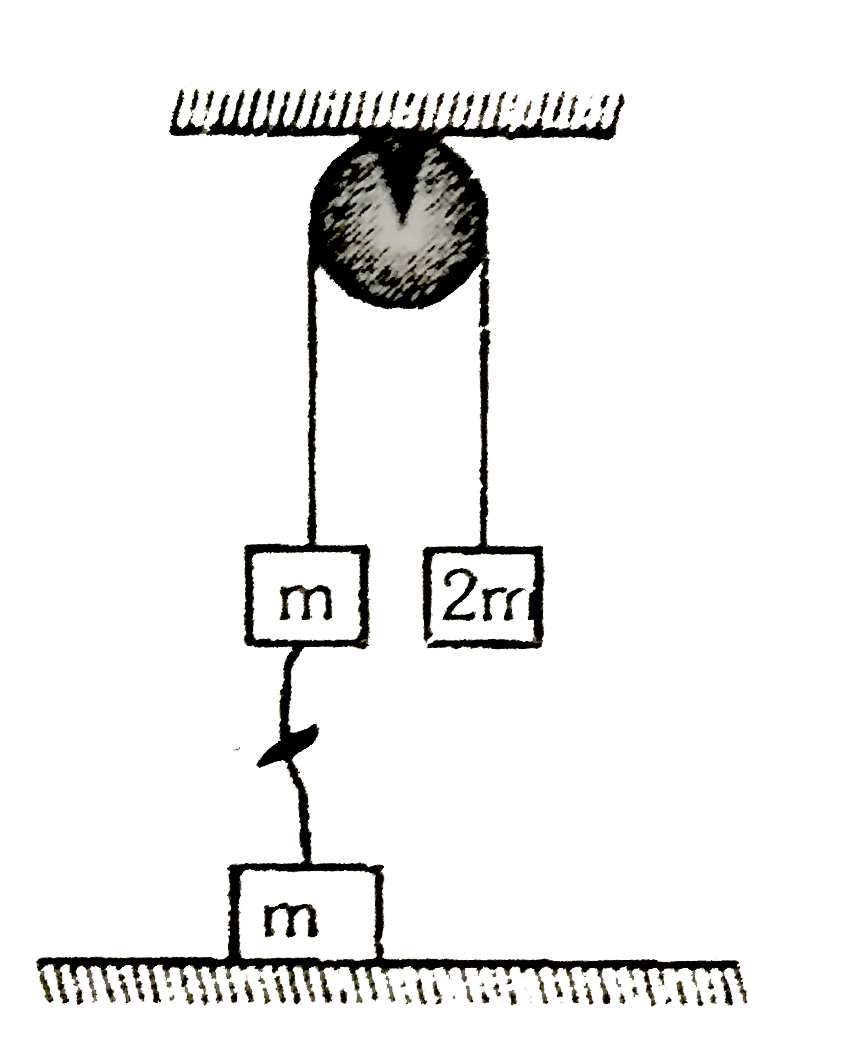Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
CENTRE OF MASS
ALLEN |Exercise EXERCISE-V A|20 VideosCENTRE OF MASS
ALLEN |Exercise EXERCISE-V B|19 VideosCENTRE OF MASS
ALLEN |Exercise EXERCISE-IV A|32 VideosBASIC MATHEMATICS USED IN PHYSICS &VECTORS
ALLEN |Exercise EXERCISE-IV ASSERTION & REASON|11 VideosELASTICITY, SURFACE TENSION AND FLUID MECHANICS
ALLEN |Exercise Exercise 5 B (Integer Type Questions)|3 Videos
Similar Questions
Explore conceptually related problems
ALLEN -CENTRE OF MASS-EXERCISE-IV B
- A bullet of mass M is fired with a velocity 50m//s at an angle with th...
Text Solution
|
- An object of mass 5 kg is projecte with a velocity of 20ms^(-1) at an ...
Text Solution
|
- Two blocks of masses m(1) and m(2) are connected by a massless pulley ...
Text Solution
|
- The 4 kg sphere form rest when theta = 60^(@) strikes a block mass of ...
Text Solution
|
- Two particles A and B of mass 2m and m respectively are attached to th...
Text Solution
|
- Two particles, each of mass m, are connected by a light inextensible s...
Text Solution
|
- After a completely inelastic collision two objects of the same mass an...
Text Solution
|
- A cylindrical solid of mass 10^(-2) kg and cross-sectional area 10^(-4...
Text Solution
|
- Two particles each of mass m are connected by a light inextensible str...
Text Solution
|
- The Atwood machine in figure has a third mass attached to it by a limp...
Text Solution
|
- A wedge of mass M = 2m rests on a smooth horizontal plane. A small blo...
Text Solution
|
- A ball of mass in m= 1 kg is hung vertically by a thread of length l =...
Text Solution
|
- A 70 g ball B dropped from a height h(0) = 9m reaches a height h(2) = ...
Text Solution
|
- A ball of mass m=1kg falling vertically with a velocity v0=2m//s strik...
Text Solution
|