Home
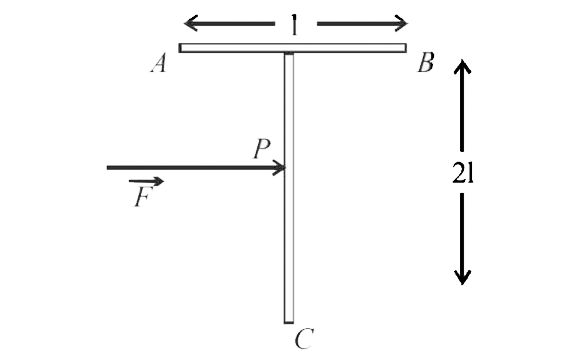
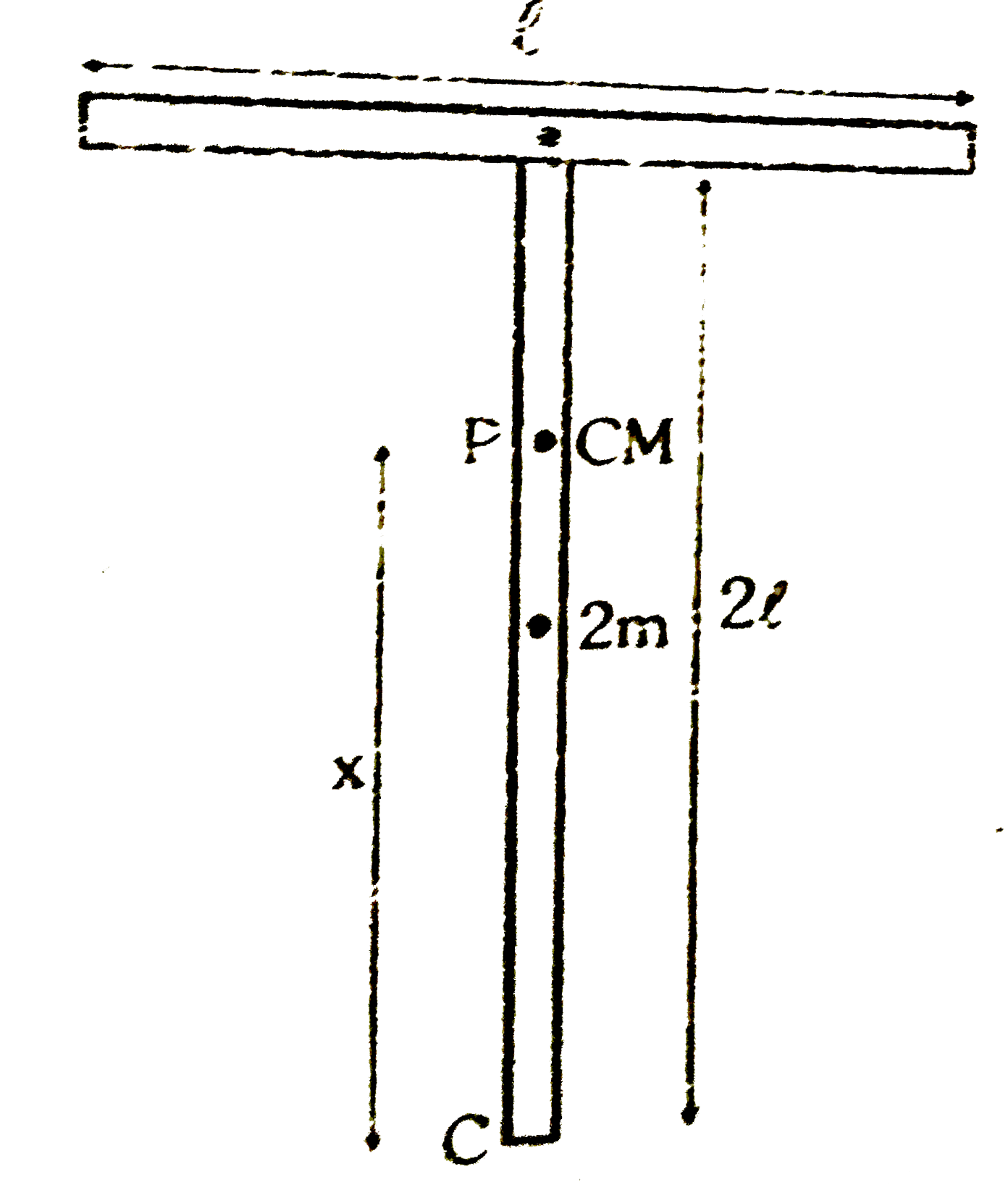Class 11
PHYSICS
A 'T' shaped object with dimensions show...

A 'T' shaped object with dimensions shown in the figure, is lying on a smooth floor. A force `'vecF'` is applied at the point P parallel to AB, such that the object has only the translational motion without rotation. Find the location of P with respect C.

A

`(2)/(3)l`

B

`(3)/(2)l`

C

`(4)/(3)l`

D

`l`

Text Solution

Verified by Experts

The correct Answer is:
C
The object will be have translation motion withour rotaion, when F is applied at CM of the system.

If P is the CM then `m(2l - x) = 2m (x - l) rArr x = (4l)/(3)`
Promotional Banner

Topper's Solved these Questions

  • CENTRE OF MASS

    ALLEN |Exercise EXERCISE-V B|19 Videos

  • CENTRE OF MASS

    ALLEN |Exercise EXERCISE-IV B|14 Videos

  • BASIC MATHEMATICS USED IN PHYSICS &VECTORS

    ALLEN |Exercise EXERCISE-IV ASSERTION & REASON|11 Videos

  • ELASTICITY, SURFACE TENSION AND FLUID MECHANICS

    ALLEN |Exercise Exercise 5 B (Integer Type Questions)|3 Videos

Similar Questions

Explore conceptually related problems

A cuboidal elevator cabon is shown in the figure. A ball is thrown from point A on the floor of cabon when the elevator is falling under gravity. The plane of motions is ABCD and the angle of projection of the ball with AB, relative to elevator, if the ball collides with point C, is alpha . Then find the value of tan alpha .

A convex lens of focal length 15 cm and a concave mirror of focal length 30 cm are kept with their optic axis PQ and RS parallel but separated in vertical directiion by 0.6 cm as shown . The distance between the lens and mirror is 30 cm . An upright object AB of height 1.2 cm is placed on the optic axis PQ of the lens at a distance of 20 cm from the lens . if A'B' is the image after refraction from the lens and the reflectiion from the mirror , find the distance of A'B' from the pole of the mirror and obtain its magnification . Also locate positions of A' and B' with respect to the optic axis RS.

A large , heavy box is sliding without friction down a smooth plane of inclination theta . From a point P on the bottom of the box , a particle is projected inside the box . The initial speed of the particle with respect to the box is u , and the direction of projection makes an angle alpha with the bottom as shown in Figure . (a) Find the distance along the bottom of the box between the point of projection p and the point Q where the particle lands . ( Assume that the particle does not hit any other surface of the box . Neglect air resistance .) (b) If the horizontal displacement of the particle as seen by an observer on the ground is zero , find the speed of the box with respect to the ground at the instant when particle was projected .

Two large plane mirrors OM and ON are arranged at 150° as shown in the figure. P is a point object and SS' is a long line perpendicular to the line OP. Find the length of the part of the line SS' on which two images of the point object P can be seen.

Two blocks of masses 6 kg and 4 kg are connected with rope of mass 2 kg are resting on a frictionless floor as shown in the following figure: If a constant force of 60N is applied to 6 kg block then the tension in the rope at points A,B and C are respectively given by :

Let y=f(x)be curve passing through (1,sqrt3) such that tangent at any point P on the curve lying in the first quadrant has positive slope and the tangent and the normal at the point P cut the x-axis at A and B respectively so that the mid-point of AB is origin. Find the differential equation of the curve and hence determine f(x).

An object A is kept fixed at the point x= 3 m and y = 1.25 m on a plank p raised above the ground . At time t = 0 the plank starts moving along the +x direction with an acceleration 1.5 m//s^(2) . At the same instant a stone is projected from the origin with a velocity vec(u) as shown . A stationary person on the ground observes the stone hitting the object during its downward motion at an angle 45(@) to the horizontal . All the motions are in the X -Y plane . Find vec(u) and the time after which the stone hits the object . Take g = 10 m//s

A vessel ABCD of 10 cm width has two small slits S_(1) and S_(2) sealed with idebtical glass plates of equal thickness. The distance between the slits is 0.8 mm . POQ is the line perpendicular to the plane AB and passing through O, the middle point of S_(1) and S_(2) . A monochromatic light source is kept at S, 40 cm below P and 2 m from the vessel, to illuminate the slits as shown in the figure. Calculate the position of the central bright fringe on the other wall CD with respect of the line OQ . Now, a liquid is poured into the vessel and filled up to OQ . The central bright fringe is fiund to be at Q. Calculate the refractive index of the liquid.

Separation of Motion of a system of particles into motion of the centre of mass and motion about the centre of mass : (a) Show p=p_(i).+m_(i)V where p_(i) is the momentum of the ith particle (of mass m_(i) ) and p_(i).=m_(i)v_(i). . Note v_(i). is the velocity of the i^(th) particle relative to the centre of mass Also, prove using the definition of the centre of mass Sigmap_(i).=0 (b) Show K=K.+(1)/(2)MV^(2) where K is the total kinetic energy of the system of particles, K. is the total kinetic energy of the system when the particle velocities are taken with respect to the centre of mass and (1)/(2)MV^(2) is the kinetic energy of the translation of the system as a whole (i.e. of the centre of mass motion of the system). The result has been used in Sec. 7.14). (c ) Show vecL=vecL.+vecRxxvec(MV) where vecL.=Sigmavec(r_(i)).xxvec(p_(i)). is the angular momentum of the system about the centre of mass with velocities taken relative to the centre of mass. Remember vec(r._(i))=vec(r_(i))-vecR , rest of the notation is the velcities taken relative to the centre of mass. Remember vec(r._(i))=vec(r_(i))-vecR rest of the notation is the standard notation used in the chapter. Note vecL , and vec(MR)xxvecV can be said to be angular momenta, respectively, about and of the centre of mass of the system of particles. (d) Show vec(dL.)/(dt)=sumvec(r_(i).)xxvec(dp.)/(dt) Further, show that vec(dL.)/(dt)=tau._(ext) where tau._(ext) is the sum of all external torques acting on the system about the centre of mass. (Hint : Use the definition of centre of mass and Newton.s Thrid Law. Assume the internal forces between any two particles act along the line joining the particles.)

Figure shows a metal rod PQ resting on the smooth rails AB and positioned between the poles of a permanent magnet. The rails, the rod, and the magnetic field are in three mutual perpendicular directions. A galvanometer G connects the rails through a switch K. Length of the rod =15 cm, B =0.50 T, resistance of the closed loop containing the rod 9.0 m Omega . Assume the field to be uniform. (a) Suppose K is open and the rod is moved with a speed of 12 "cm s"^(-1) in the direction shown. Give the polarity and magnitude of the induced emf. (b) Is there an excess charge built up at the ends of the rods when K is open ? What if K is closed ? (c) With K open and the rod moving uniformly, there is no net force on the electrons in the rod PQ even though they do experience magnetic force due to the motion of the rod. Explain. (d) What is the retarding force on the rod when K is closed ? How much power is required (by an external agent) to keep the rod moving at the same speed (= 12 cm s^(-1) ) when K is closed ? How much power is required when K is open? (f)How much power is dissipated as heat in the closed circuit ? What is the source of this power ? (g) What is the induced emf in the moving rod if the magnetic field is parallel to the rails instead of being perpendicular ?

ALLEN -CENTRE OF MASS-EXERCISE-V A
  1. Two identical particles move towards each other with velocity 2v and v...

    Text Solution

    |

  2. Consider the following two statements: A. Linear momentum of a syste...

    Text Solution

    |

  3. Two spherical bodies of mass M and 5M & radii R and 2R respectively, a...

    Text Solution

    |

  4. A body A of mass M while falling wertically downwards under gravity br...

    Text Solution

    |

  5. The block of mass M moving on the frictionless horizontal surface col...

    Text Solution

    |

  6. A mass 'm' moves with a velocity 'v' and collides inelastieally with a...

    Text Solution

    |

  7. A 'T' shaped object with dimensions shown in the figure, is lying on a...

    Text Solution

    |

  8. A bomb of mass 16kg at rest explodes into two pieces of masses 4 kg an...

    Text Solution

    |

  9. Consider a two particle system with particles having masses m(1)andm(2...

    Text Solution

    |

  10. A circular disc of radius R is removed from a bigger circular disc of ...

    Text Solution

    |

  11. A block of mass 0.50kg is moving with a speed of 2.00m//s on a smooth ...

    Text Solution

    |

  12. A thin rod of length 6 m is lying along the x-axis with its ends at x=...

    Text Solution

    |

  13. Consider a rubber ball freely falling from a height h = 4.9 m onto a ...

    Text Solution

    |

  14. Statement -1: Two particles moving in the same direction do not lose a...

    Text Solution

    |

  15. This question has statement -I and statement - II of the four choices...

    Text Solution

    |

  16. Distance of the centre of mass of a solid uniform cone from its vertex...

    Text Solution

    |

  17. A particle of mass m moving in the x - direction with speed 2c is hit...

    Text Solution

    |

  18. A uniform thin rod AB of length L has linear mass density mu(x) = a + ...

    Text Solution

    |

  19. A large number (n) of identical beads, each of mass m and radius r are...

    Text Solution

    |

  20. In the figure shown ABC is a uniform wire. If centre of mass of wire l...

    Text Solution

    |