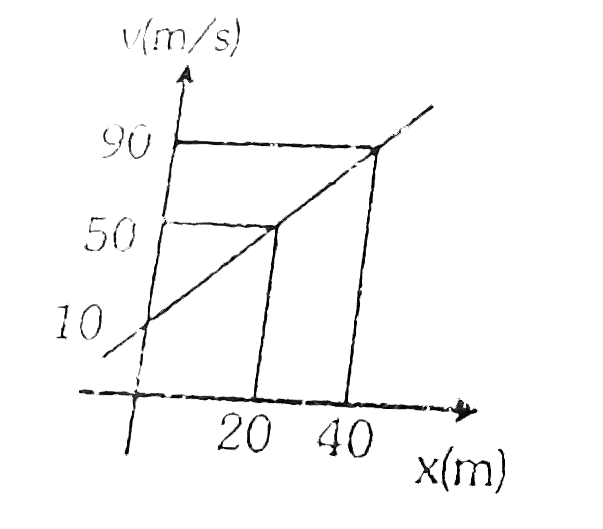Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
MISCELLANEOUS
ALLEN |Exercise Exersice-4[B]|14 VideosMISCELLANEOUS
ALLEN |Exercise EXERCISE-5(A)|15 VideosMISCELLANEOUS
ALLEN |Exercise DATA SUFFICIENCY QUESTIONS|3 VideosKINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)
ALLEN |Exercise BEGINNER S BOX-7|8 VideosPHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT
ALLEN |Exercise EXERCISE-IV|7 Videos
Similar Questions
Explore conceptually related problems
ALLEN -MISCELLANEOUS-Exercise-04 [A]
- The position vector of car w.r.t. its starting point is given as vecr=...
Text Solution
|
- Answer the following : (i) A vector has magnitude & direction. Does ...
Text Solution
|
- A room has dimensions 3 m xx 4 m xx5 m. A fly starting at one cronet e...
Text Solution
|
- Vector vec(a) has components a(x)=3, a(y)=4. Find the components of a ...
Text Solution
|
- Find: (i) "north cross west" " " (ii) "down dot south" (iii) "we...
Text Solution
|
- The position vector of a particle of mass m= 6kg is given as vec(r)=[(...
Text Solution
|
- A plane body has perpendicular axes OX and OY marked on it and is acte...
Text Solution
|
- State with reasons, whether the following algebraic operations with sc...
Text Solution
|
- A car travels due east on a level road for 30 km. It then turns due no...
Text Solution
|
- Write the vector representation of the vectors A and B with respect to...
Text Solution
|
- Find the kinetic energy of a particle of mass 200 g moving with veloci...
Text Solution
|
- Acceleration of particle moving in straight line can be written as a=(...
Text Solution
|
- The position vector of an object moving in X-Z plane is vec(r)=v(0)tha...
Text Solution
|
- The position of a particle at time t is given by the relation x(t)=((V...
Text Solution
|
- The related equations are : Q=mc(T(2)-T(1)), l(1)=l(0)[1+alpha(T(2)-T(...
Text Solution
|
- A particle of mass m is in a uni-directional potential field where the...
Text Solution
|
- Assume that the largest stone of mass 'm' that can be moved by a flowi...
Text Solution
|
- A projectile fired at an angle of 45^(@) travels a total distance R, c...
Text Solution
|
- In the formula P=(nRT)/(V-b)e^(-a/(RTV)). Find the dimensions of a and...
Text Solution
|
- If instead of mass, length and time as fundamental quantities we choos...
Text Solution
|