Home
Class 11
PHYSICS
A bullet of mass m and charge q is fired...

A bullet of mass m and charge q is fired towards a solid uniformly charge sphere of radius R and total charge +q. If it strikes the surface of sphere with speed u, find the minimum value of u so that it can penetrate through the sphere. (Neglect all resistance force or friction acting on bullet except electrostatic forces)

A

`q/sqrt(2piepsilon_(0)mR)`

B

`q/sqrt(4piepsilon_(0)mR)`

C

`q/sqrt(8piepsilon_(0)mR)`

D

`(sqrt(3)q)/sqrt(4piepsilon_(0)mR)`

Text Solution

Verified by Experts

The correct Answer is:
B
Energy at surface = Energy at centre
`1/2 m u^(2)+(Kqxxq)/R=3/2 (Kq)/(R)xxq+0`
`:. U=q/sqrt(4pi in_(0)mR)`
Promotional Banner

Topper's Solved these Questions

  • MISCELLANEOUS

    ALLEN |Exercise Exercise-03|1 Videos

  • MISCELLANEOUS

    ALLEN |Exercise Exercise-04|1 Videos

  • MISCELLANEOUS

    ALLEN |Exercise Exersice -05(B)|20 Videos

  • KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)

    ALLEN |Exercise BEGINNER S BOX-7|8 Videos

  • PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT

    ALLEN |Exercise EXERCISE-IV|7 Videos

Similar Questions

Explore conceptually related problems

A particle of mass m and charge -q moves along a diameter of a uniformly charged sphere of radius R and carrying a total charge +Q . Find the frequency of S.H.M. of the particle if the amplitude does not exceed R .

A positive charge Q is uniformly distributed throughout the volume of a dielectric sphere of radius R. A point mass having charge +q and mass m is fired toward the center of the sphere with velocity v from a point at distance r (r gt R) from the center of the sphere. Find the minimum velocity v so that it can penetrate (R//2) distance of the sphere. Neglect any resistance other than electric interaction. Charge on the small mass remains constant throughout the motion.

Let P(r)=(Q)/(piR^4)r be the charge density distribution for a solid sphere of radius R and total charge Q. For a point 'p' inside the sphere at distance r_1 from the centre of the sphere, the magnitude of electric field is:

Q amount of electric charge is present on the surface of a sphere having radius R. Calculate the total energy of the system.

In a uniformly charges sphere of total charge Q and radius R, the electric field E is plotted as a function of distance from the centre. The graph which would corresponding to the above will be :-

An insulating solid sphere of radius R has a uniformaly positive charge density rho . As a result of this uniform charge distribution there is a finite value of electric potential at the centre of the sphere, at the surface of the sphere and also at a point out side the sphere. The electric potential at infinity is zero. Statement-1: Wgen a charge 'q' is taken from the centre to the surface of the sphere, its potential energy charges by (qrho)/(3 in_(0)) Statement-2 : The electric field at a distance r (r lt R) from the centre of the the sphere is (rho r)/(3in_(0))

An accelration produces a narrow beam of protons, each having an initial speed of v_(0) . The beam is directed towards an initially uncharges distant metal sphere of radius R and centered at point O. The initial path of the beam is parallel to the axis of the sphere at a distance of (R//2) from the axis, as indicated in the diagram. The protons in the beam that collide with the sphere will cause it to becomes charged. The subsequentpotential field at the accelerator due to the sphere can be neglected. The angular momentum of a particle is defined in a similar way to the moment of a force. It is defined as the moment of its linear momentum, linear replacing the force. We may assume the angular momentum of a proton about point O to be conserved. Assume the mass of the proton as m_(P) and the charge on it as e. Given that the potential of the sphere increases with time and eventually reaches a constant velue. One the potential of the sphere has reached its final, constant value, the minimum speed v of a proton along its trajectory path is given by

An accelration produces a narrow beam of protons, each having an initial speed of v_(0) . The beam is directed towards an initially uncharges distant metal sphere of radius R and centered at point O. The initial path of the beam is parallel to the axis of the sphere at a distance of (R//2) from the axis, as indicated in the diagram. The protons in the beam that collide with the sphere will cause it to becomes charged. The subsequentpotential field at the accelerator due to the sphere can be neglected. The angular momentum of a particle is defined in a similar way to the moment of a force. It is defined as the moment of its linear momentum, linear replacing the force. We may assume the angular momentum of a proton about point O to be conserved. Assume the mass of the proton as m_(P) and the charge on it as e. Given that the potential of the sphere increases with time and eventually reaches a constant velue. After a long time, when the potential of the sphere reaches a constant value, the trajectory of proton is correctly sketched as

An accelration produces a narrow beam of protons, each having an initial speed of v_(0) . The beam is directed towards an initially uncharges distant metal sphere of radius R and centered at point O. The initial path of the beam is parallel to the axis of the sphere at a distance of (R//2) from the axis, as indicated in the diagram. The protons in the beam that collide with the sphere will cause it to becomes charged. The subsequentpotential field at the accelerator due to the sphere can be neglected. The angular momentum of a particle is defined in a similar way to the moment of a force. It is defined as the moment of its linear momentum, linear replacing the force. We may assume the angular momentum of a proton about point O to be conserved. Assume the mass of the proton as m_(P) and the charge on it as e. Given that the potential of the sphere increases with time and eventually reaches a constant velue. The limiting electric potential of the sphere is

An accelration produces a narrow beam of protons, each having an initial speed of v_(0) . The beam is directed towards an initially uncharges distant metal sphere of radius R and centered at point O. The initial path of the beam is parallel to the axis of the sphere at a distance of (R//2) from the axis, as indicated in the diagram. The protons in the beam that collide with the sphere will cause it to becomes charged. The subsequentpotential field at the accelerator due to the sphere can be neglected. The angular momentum of a particle is defined in a similar way to the moment of a force. It is defined as the moment of its linear momentum, linear replacing the force. We may assume the angular momentum of a proton about point O to be conserved. Assume the mass of the proton as m_(P) and the charge on it as e. Given that the potential of the sphere increases with time and eventually reaches a constant velue. If the initial kinetic energy of a proton is 2.56 ke V , then the final potential of the sphere is

ALLEN -MISCELLANEOUS-Exercise-02
  1. The dipole moment of a system of charge +q distribyted uniformly on a...

    Text Solution

    |

  2. An electric dipole is kept on the axis of a uniformly charged ring at ...

    Text Solution

    |

  3. Point P lies on the axis of a dipole . If the dipole is rotated by 90...

    Text Solution

    |

  4. Two short electric dipole are placed as shown. The energy of electric ...

    Text Solution

    |

  5. Charges Q1 and Q2 lie inside and outside, respectively, of a closed su...

    Text Solution

    |

  6. An electric dipole is placed at the centre of a sphere. Mark the corre...

    Text Solution

    |

  7. An infinite, uniformly charged sheet with surface charge density sigma...

    Text Solution

    |

  8. At a distance of 5 cm and 10 cm outward from the surface of a uniforml...

    Text Solution

    |

  9. An electric field converges at the origin whose magnitude is given by ...

    Text Solution

    |

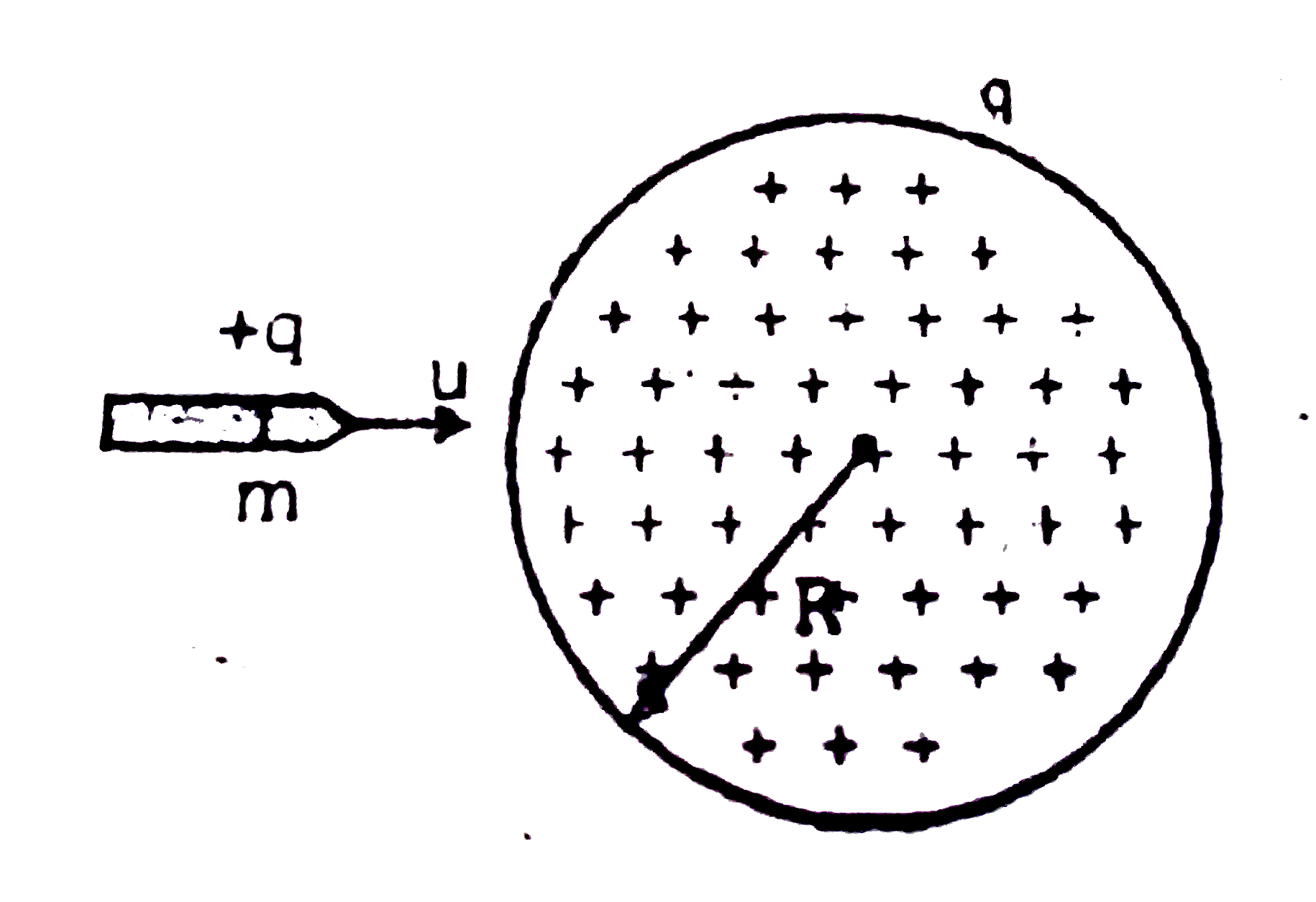
  10. A bullet of mass m and charge q is fired towards a solid uniformly cha...

    Text Solution

    |

  11. A unit positive point charge of mass m is projected with a velocity v ...

    Text Solution

    |

  12. Three concentric conducting spherical shells have radii r, 2r, and 3r ...

    Text Solution

    |

  13. Shown in the figure a spherical shell with an inner radius 'a' and an ...

    Text Solution

    |

  14. In the previous question assume that the electrostatic potential is ze...

    Text Solution

    |

  15. There are four concentric shells A,B, C and D of radii a,2a,3a and 4a ...

    Text Solution

    |

  16. X and Y are large, parallel conducting plates close to each other. Eac...

    Text Solution

    |

  17. Plates a and B constitutes an isolated, charge parallel plate capacito...

    Text Solution

    |

  18. A wheel having mass m has charges + q and - q on diametrically opposit...

    Text Solution

    |

  19. A tiny charged pellet of mass m is suspended at rest by the electric f...

    Text Solution

    |

  20. A positive point charge is placed at P in front of an earthed metal sh...

    Text Solution

    |