Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
MISCELLANEOUS
ALLEN |Exercise Exersice-04[B]|16 VideosMISCELLANEOUS
ALLEN |Exercise Exercise-05(A)|35 VideosMISCELLANEOUS
ALLEN |Exercise Comprehension 9|2 VideosKINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)
ALLEN |Exercise BEGINNER S BOX-7|8 VideosPHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT
ALLEN |Exercise EXERCISE-IV|7 Videos
Similar Questions
Explore conceptually related problems
ALLEN -MISCELLANEOUS-Exersice-04[A]
- Three particles, each of mass m and carrying a charge q each, are susp...
Text Solution
|
- Two equal point charges Q=+sqrt(2) mu C are placed at each of the two ...
Text Solution
|
- A point charge 4 is situated at a distance r on axis from one end of ...
Text Solution
|
- A thin circular wire of radius r has a charge Q. If a point charge q i...
Text Solution
|
- An infinite number of charges, each equal to Q=10 mu C are placed alon...
Text Solution
|
- The figure shows three infinite non-conducting plates of charge perpen...
Text Solution
|
- Find the electric field at centre of semicircular ring shown in figure...
Text Solution
|
- what is the dimension of moment of ineartia?
Text Solution
|
- Two concentric rings, one of radius a and the other of radius b, have ...
Text Solution
|
- In the figure shown S is a large nonconducting sheet of uniform charge...
Text Solution
|
- root(4)(16)xxroot(4)(2) is equal t :-
Text Solution
|
- Consider the configuration of a system of four charges each of value (...
Text Solution
|
- Which of the following has different dimensional formula ?
Text Solution
|
- Which of the following has different dimensional formula ?
Text Solution
|
- root(5)(64)××root(6)(2) is equal to :-
Text Solution
|
- Three point charges q, 2q and 8q are to be placed on a . 9cm long st...
Text Solution
|
- A charge +Q is uniformly distributed over a thin ring with radius R....
Text Solution
|
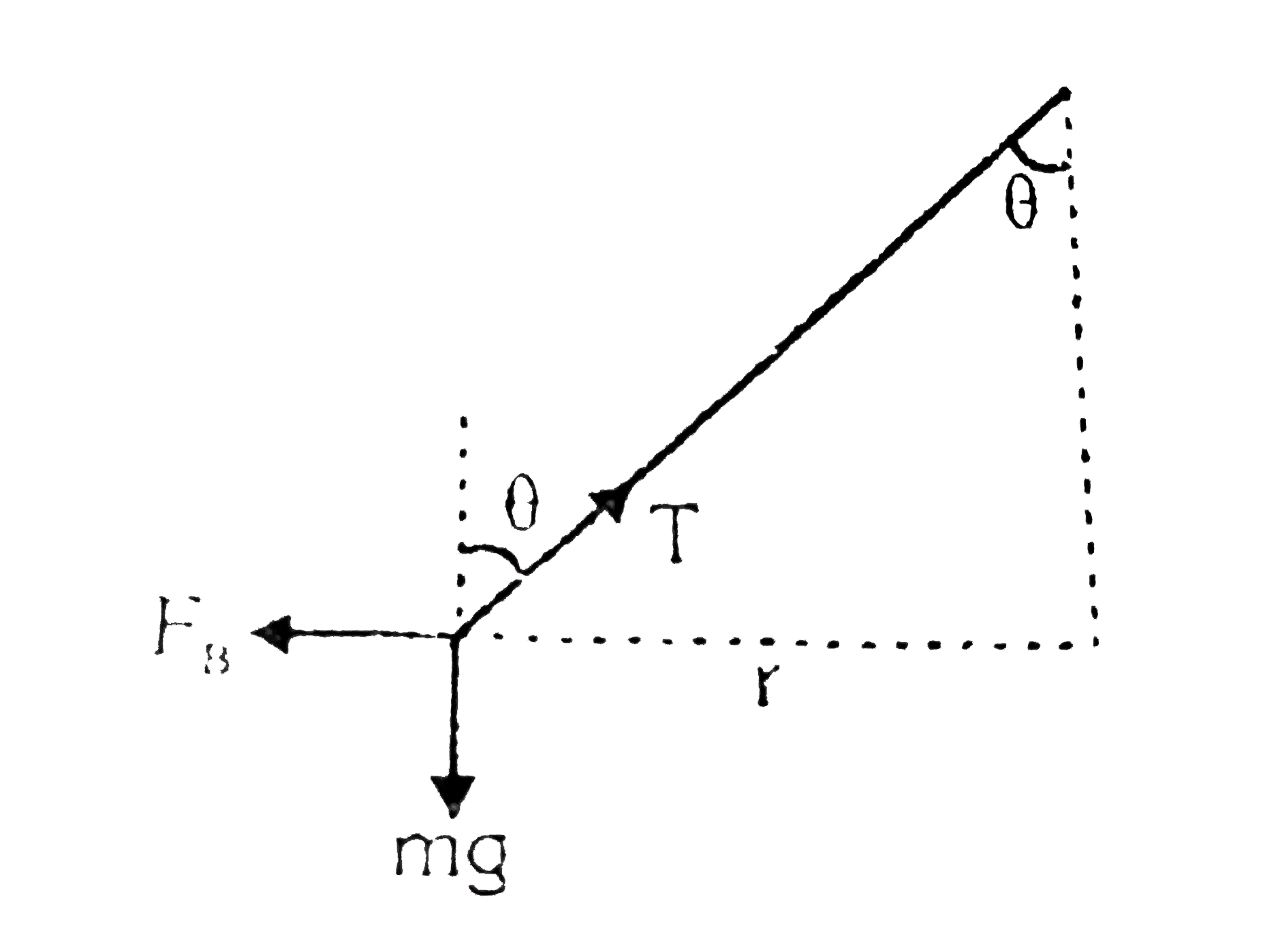
- A simple pendulum of length l and bob mass m is hanging in front of a ...
Text Solution
|
- Two fixed, equal, positive charges, each of magnitude 5xx10^-5 coul ar...
Text Solution
|
- Positive and negative charges of 1 muC each are placed at two points a...
Text Solution
|