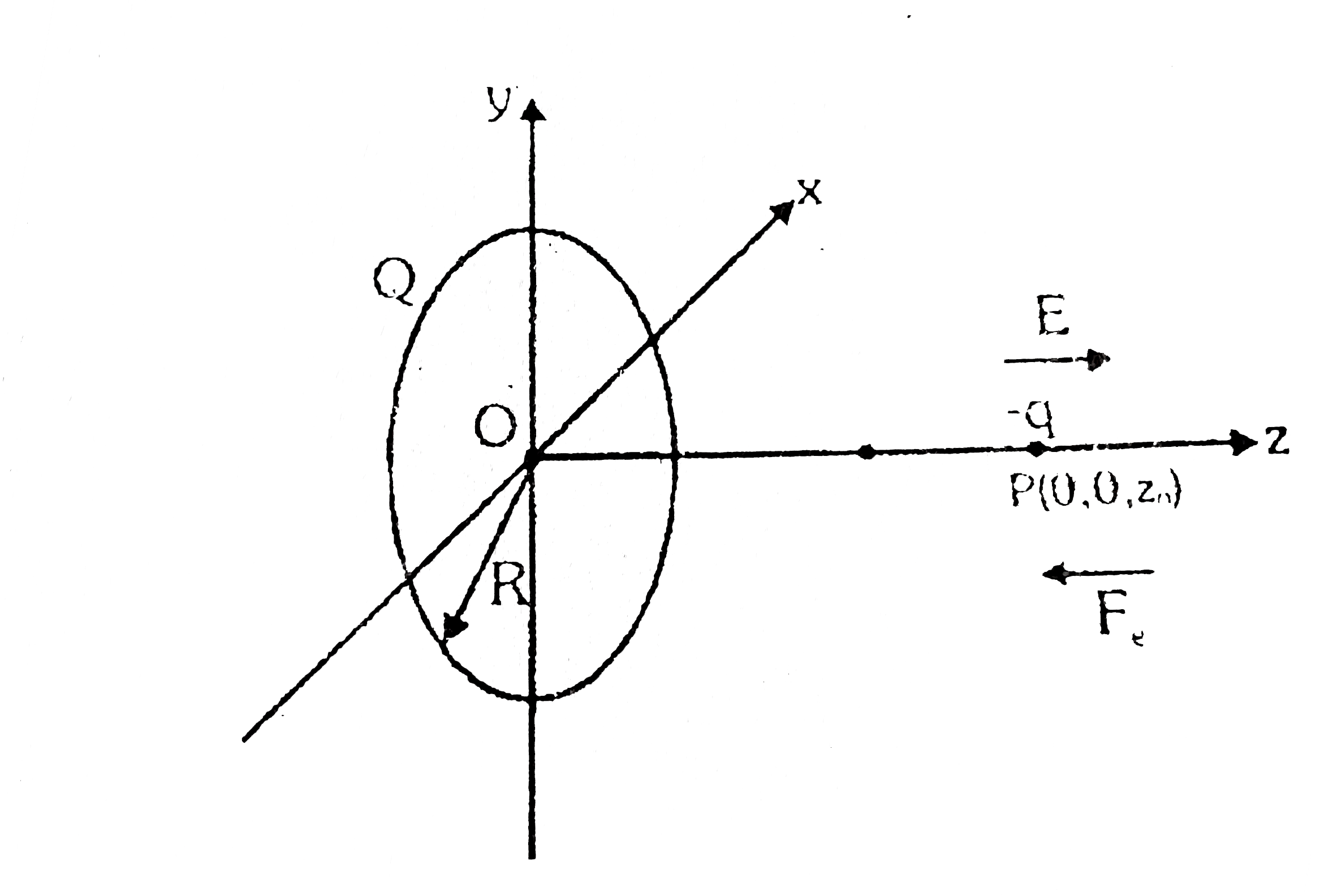A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
MISCELLANEOUS
ALLEN |Exercise REASONING TYPE|1 VideosMISCELLANEOUS
ALLEN |Exercise MATCH THE COLUME TYPE|1 VideosMISCELLANEOUS
ALLEN |Exercise Exercise-05(B)|19 VideosKINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)
ALLEN |Exercise BEGINNER S BOX-7|8 VideosPHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT
ALLEN |Exercise EXERCISE-IV|7 Videos
Similar Questions
Explore conceptually related problems
ALLEN -MISCELLANEOUS-MCQ s WITH ONE OR MORE THAN ONE CORRECT ANSWER
- A positively charged thin metal ring of radius R is fixed in the xy pl...
Text Solution
|
- A non-conducting solid sphere of radius R is uniformly charged. The ma...
Text Solution
|
- An ellipsoidal cavity is carved within a perfect conductor. A positive...
Text Solution
|
- For spherical symmetrical charge distribution, variation of electric p...
Text Solution
|
- Two non-conducting solid spheres of radii R and 2R, having uniform vol...
Text Solution
|
- Two non-conducting spheres of radii R1 and R2 and carrying uniform vol...
Text Solution
|