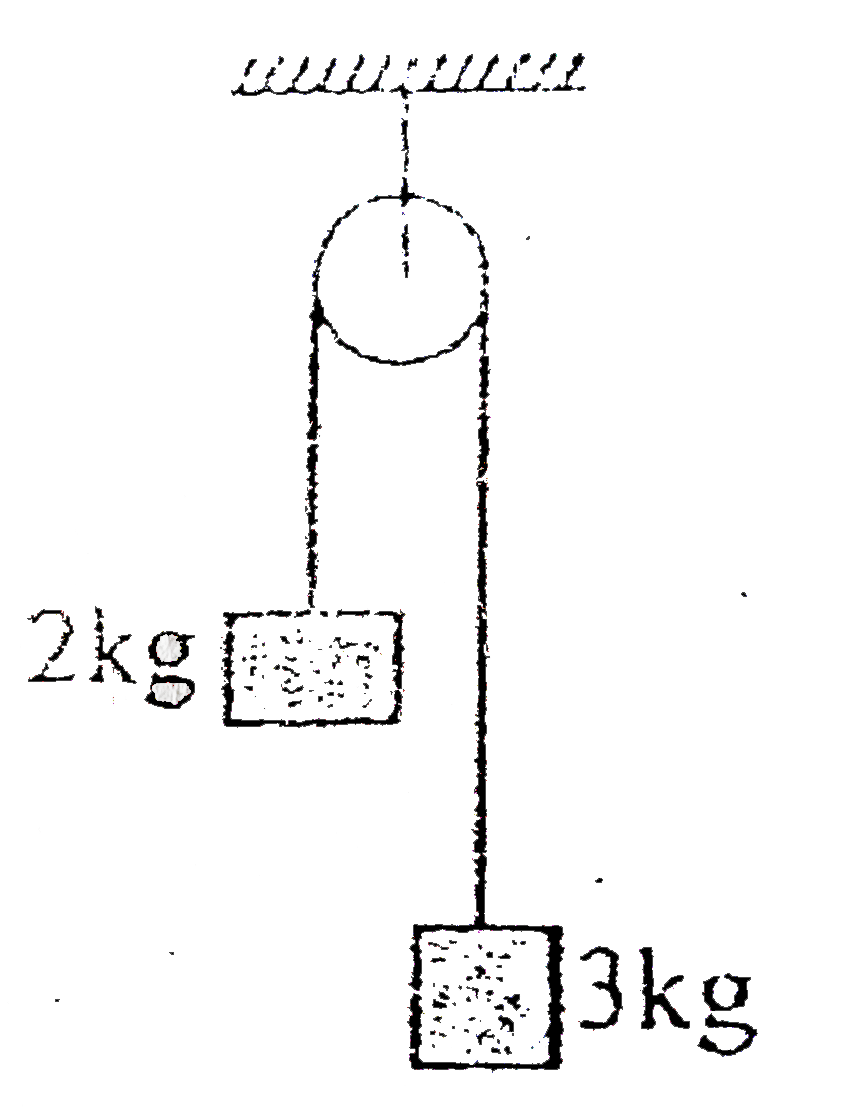Home
Class 12
PHYSICS
In the ideal atwood machine arrangement ...

In the ideal atwood machine arrangement shown, what is the change in kinetic energy of the system in `(1)/(sqrt2)`second of their motion starting from rest ?

A

`1J`

B

`2J`

C

`4J`

D

`5J`

Text Solution

Verified by Experts

The correct Answer is:
D
Acceleration`=(3g-2g)/(5)=2m//s^(2)` so
`v=2xx(1)/(sqrt2)=sqrt2m//s`
`:.DeltaE=(1)/(2)(2)(sqrt2)^(2)+(1)/(2)(3)(sqrt2)^(2)=5`
Promotional Banner

Topper's Solved these Questions

Similar Questions

Explore conceptually related problems

An electron and a proton are moving under the influence of mutual forces . In calculating the change in the kinetic energy of the system during motion , one ignores the magnetic force of one on another . This is , because

The graph below shows how the force on a mass depends on the position of the mass. What is the change in the kinetic energy of the mass as it moves from x=0.0m to x=3.0 m ?

In the balance machine shown in the figures. Which arm will move downward after the system is released from rest (assuming stiring, arm of balance machie and the pulley to be light)

If y=x^(4)-10 and if x change from 2 to 1.99, what is the change in y ……….

Two disc of moments of inertia I_(1)andI_(2) about their respective axes (normal to the disc and passing through the centre), and rotating with angular speeds omega_(1)andomega_(2) are brought into contact face to face with their axes of rotation coincident. (a) What is the angular speed of the two-disc system? (b) Show that the kinetic energy of the combined system is less than the sum of the initial kinetic energies of the two discs. How do you account for this loss in energy? Take omega_(1)neomega_(2) .

Two discs of moments of inertia I_(1) and I_(2) about their respective axes (normal to the disc and passing through the centre), and rotating with angular speeds ω_(1) and ω_(2) are brought into contact face to face with their axes of rotation coincident. (a) What is the angular speed of the two-disc system? (b) Show that the kinetic energy of the combined system is less than the sum of the initial kinetic energies of the two discs. How do you account for this loss in energy? Take omega_(1)neomega_(2)

A particle of mass 10 g moves along a circle of radius 6.4 cm with constant tangential acceleration. What is the magnitude of this acceleration if the kinetic energy of the particle becomes equal 8xx10^(-4)J by the end of the second revolution after the beginning of the motion?

A cord of negligible mass is wound round the rim of a fly wheel of mass 20 kg and radius 20 cm. A steady pull of 25 N is applied on the cord as shown in Fig. 7.35. The flywheel is mounted on a horizontal axle with frictionless bearings. (a) Compute the angular acceleration of the wheel. (b) Find the work done by the pull, when 2m of the cord is unwound. (c) Find also the kinetic energy of the wheel at this point. Assume that the wheel starts from rest. (d) Compare answers to parts (b) and (c).

Separation of Motion of a system of particles into motion of the centre of mass and motion about the centre of mass : (a) Show p=p_(i).+m_(i)V where p_(i) is the momentum of the ith particle (of mass m_(i) ) and p_(i).=m_(i)v_(i). . Note v_(i). is the velocity of the i^(th) particle relative to the centre of mass Also, prove using the definition of the centre of mass Sigmap_(i).=0 (b) Show K=K.+(1)/(2)MV^(2) where K is the total kinetic energy of the system of particles, K. is the total kinetic energy of the system when the particle velocities are taken with respect to the centre of mass and (1)/(2)MV^(2) is the kinetic energy of the translation of the system as a whole (i.e. of the centre of mass motion of the system). The result has been used in Sec. 7.14). (c ) Show vecL=vecL.+vecRxxvec(MV) where vecL.=Sigmavec(r_(i)).xxvec(p_(i)). is the angular momentum of the system about the centre of mass with velocities taken relative to the centre of mass. Remember vec(r._(i))=vec(r_(i))-vecR , rest of the notation is the velcities taken relative to the centre of mass. Remember vec(r._(i))=vec(r_(i))-vecR rest of the notation is the standard notation used in the chapter. Note vecL , and vec(MR)xxvecV can be said to be angular momenta, respectively, about and of the centre of mass of the system of particles. (d) Show vec(dL.)/(dt)=sumvec(r_(i).)xxvec(dp.)/(dt) Further, show that vec(dL.)/(dt)=tau._(ext) where tau._(ext) is the sum of all external torques acting on the system about the centre of mass. (Hint : Use the definition of centre of mass and Newton.s Thrid Law. Assume the internal forces between any two particles act along the line joining the particles.)

ALLEN -TEST PAPER-Exercise (Physics)
  1. A particle A is projected verically upwards. Another indentical partic...

    Text Solution

    |

  2. Track OABCD (as shown is figure) is smooth and fixed in vertical plane...

    Text Solution

    |

  3. In the ideal atwood machine arrangement shown, what is the change in k...

    Text Solution

    |

  4. A partical of mass 2kg is moving on the x-axis with a constant mechani...

    Text Solution

    |

  5. A chain of length L and mass m is placed upon a smooth surface. The le...

    Text Solution

    |

  6. Potential energy function along x-axis in a certain force field is giv...

    Text Solution

    |

  7. A pigeon in flight experience a force of air resistance given by F=bv^...

    Text Solution

    |

  8. A potential energy curve U(x) is shown in the figure. What value must ...

    Text Solution

    |

  9. The left end of the spring tied to a wall and at the right end is atta...

    Text Solution

    |

  10. A block weighing 40N travels down a smooth fixed curved track AB joine...

    Text Solution

    |

  11. Two atoms interact with each other according to the following force F ...

    Text Solution

    |

  12. The potential energy U(x) of a particle moving along x-axis is shown i...

    Text Solution

    |

  13. A particle is to move along the x-axis from x=0 to x=x(1) while a cons...

    Text Solution

    |

  14. A body with mass 2kg moves in one direction in the presence of a force...

    Text Solution

    |

  15. An escalator is used to move 5 people (60kg each) per minute from the ...

    Text Solution

    |

  16. A stone is dropped into a quiet lake and waves move in circles at the ...

    Text Solution

    |

  17. For conservative force field, vec(F)=-(delU)/(delx)hat(i)-(delU)/(dy)...

    Text Solution

    |

  18. Find the value of x(1), so that int(0)^(x(1))ydx=5

    Text Solution

    |

  19. A rocket rises vertically up from the surface of earth so that it is d...

    Text Solution

    |

  20. Find the rate of change of radius of a sphere when its radius is 4 cm ...

    Text Solution

    |