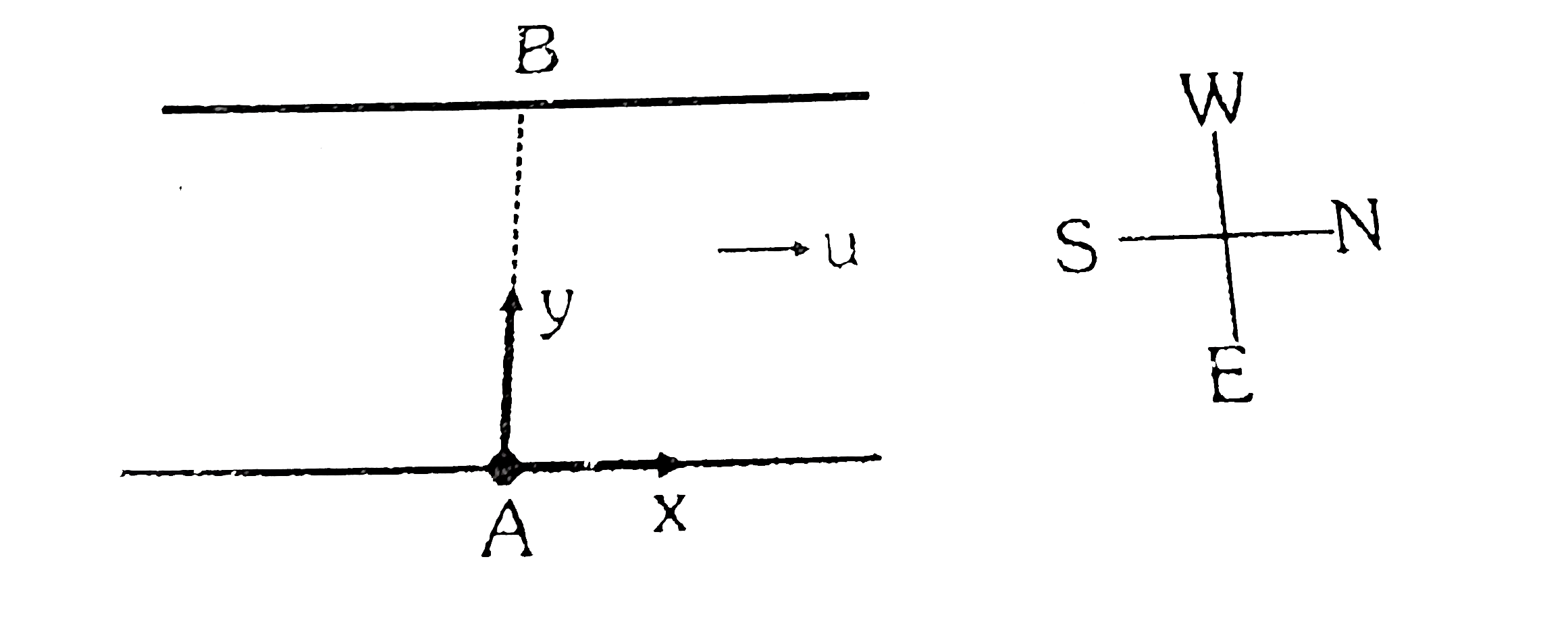A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
ALLEN -KINEMATICS-EXERCISE-2
- A river of width 'd' with straight parallel banks flows due North with...
Text Solution
|
- A student performs an experiment to determine how the range of a ball ...
Text Solution
|
- A student performs an experiment to determine how the range of a ball ...
Text Solution
|
- A student performs an experiment to determine how the range of a ball ...
Text Solution
|
- A circus wishes to develop a new clown act. Fig. (1) shows a diagram o...
Text Solution
|
- A circus wishes to develop a new clown act. Fig. (1) shows a diagram o...
Text Solution
|
- A circus wishes to develop a new clown act. Fig. (1) shows a diagram o...
Text Solution
|
- A circus wishes to develop a new clown act. Fig. (1) shows a diagram o...
Text Solution
|
- A circus wishes to develop a new clown act. Fig. (1) shows a diagram o...
Text Solution
|
- A circus wishes to develop a new clown act. Fig. (1) shows a diagram o...
Text Solution
|
- When a particle is undergoing motion, the diplacement of the particle ...
Text Solution
|
- When a particle is undergoing motion, the diplacement of the particle ...
Text Solution
|
- When a particle is undergoing motion, the diplacement of the particle ...
Text Solution
|
- When a particle is undergoing motion, the diplacement of the particle ...
Text Solution
|
- A projectile is projected with some initial velocity and some initial ...
Text Solution
|
- A projectile is projected with some initial velocity and some initial ...
Text Solution
|
- A projectile is projected with some initial velocity and some initial ...
Text Solution
|
- Fig. 2 (NCT).9 show the x-t plot of a particle in one dimensional mot...
Text Solution
|
- The position-time(x-t) graphs for two children A and B from their sch...
Text Solution
|
- A particle moves along x-axis with acceleration a = a0 (1 – t// T) wh...
Text Solution
|
- A body moving with uniform acceleration, covers a distance of 20 m in ...
Text Solution
|