Home
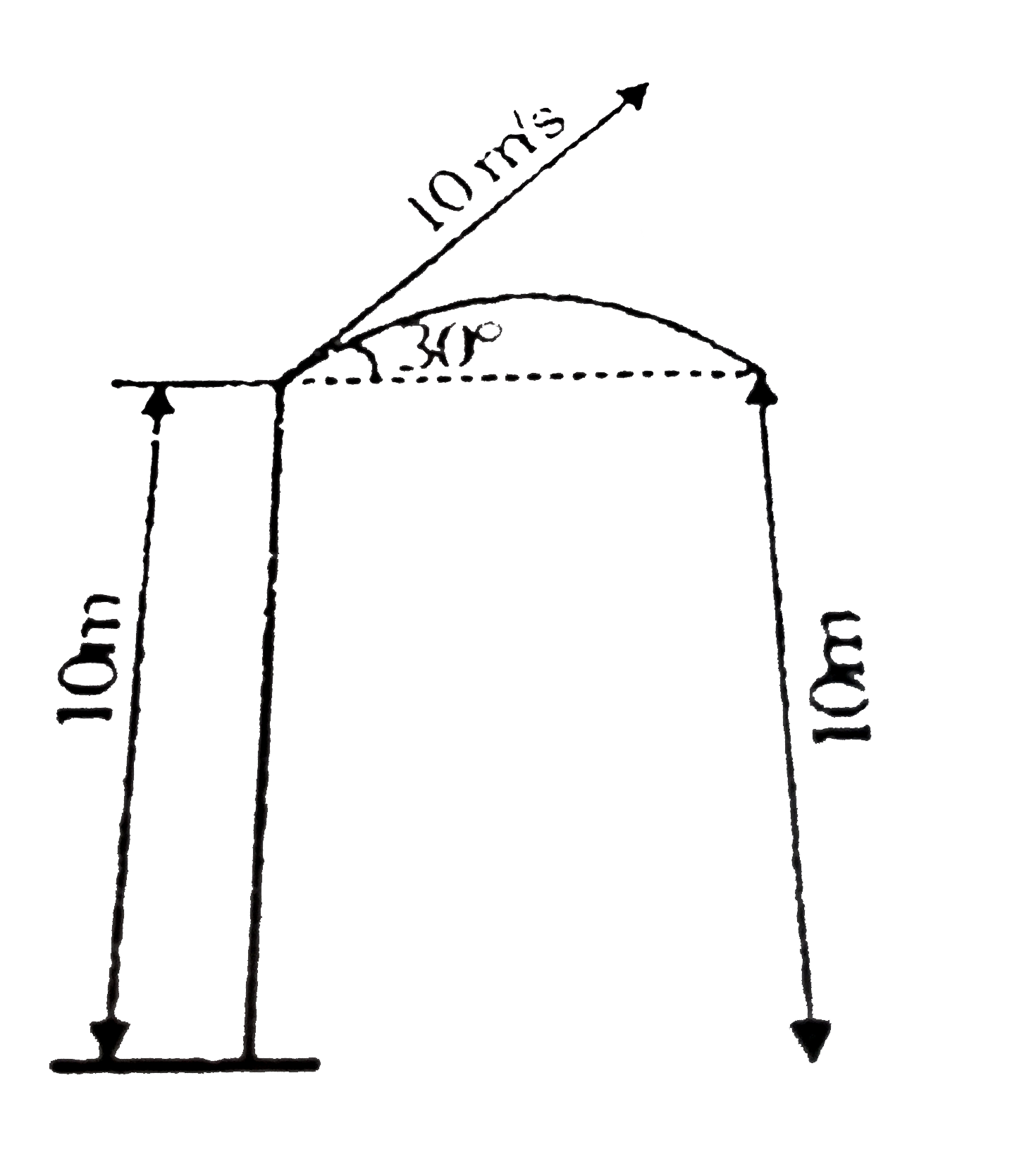
Class 11
PHYSICS
A boy playing on the roof of a 10 m high...

A boy playing on the roof of a `10 m` high building throws a ball with a speed of `10 m//s` at an angle of `30(@)` with the horizontal. How far from the throwing point will the ball be at the height of `10 m` from the ground ?
`[ g = 10m//s^(2) , sin 30^(@) = (1)/(2) , cos 30^(@) = (sqrt(3))/(2)]`

A

5.20 m

B

4.33 m

C

2.60 m

D

8.66 m

Text Solution

Verified by Experts

The correct Answer is:
4
`R=(u^(2) sin 2theta)/g`
`R=((10)^(2) sin 60^(@))/10`
`R=10xxsqrt(3)/2=5sqrt(3)=8.66 m`
Promotional Banner

Topper's Solved these Questions

  • KINEMATICS

    ALLEN |Exercise Exercise-05[B]|5 Videos

  • KINEMATICS

    ALLEN |Exercise MCQ with one or more than one correct Question|1 Videos

  • KINEMATICS

    ALLEN |Exercise Exercise-04[B]|14 Videos

  • ERROR AND MEASUREMENT

    ALLEN |Exercise Part-2(Exercise-2)(B)|22 Videos

  • KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)

    ALLEN |Exercise BEGINNER S BOX-7|8 Videos

Similar Questions

Explore conceptually related problems

A particle is projected with a velocity 10 m/s at an angle 37^(@) to the horizontal. Find the location at which the particle is at a height 1 m from point of projection.

A train is moving along a straight line with a constant acceleration 'a' . A boy standing in the train throws a ball forward with a speed of 10 m//s , at an angle of 60(@) to the horizontal. The boy has to move forward by 1.15 m inside the train to catch the ball back at the initial height . the acceleration of the train , in m//s^(2) , is

A ball is projected upwards from the top of a tower with a velocity 50ms^-1 making an angle 30^@ with the horizontal. The height of tower is 70m. After how many seconds from the instant of throwing, will the ball reach the ground. (g=10 ms^-2)

A golfer standing on level ground hits a ball with a velocity of u=52m//s at an angle alpha above the horizontal. If tantheta=5//12 , then the time interval for which the ball is at least 15 m above the ground (i.e. between A and B will be :(take g=10m//s^(2) )

A ball is thrown from the top of 36m high tower with velocity 5m//ss at an angle 37^(@) above the horizontal as shown. Its horizontal distance on the ground is closest to [ g=10m//s^(2) :

The top of two poles of height 16m and 10m are connected by a wire. If the wire makes an angle of 30^(@) with the horizontal, then its length is……….m

Find the speed of a body at the ground when it fall freely at height 2m . ( g = 10 ms^(-2))

A ball is thrown upwards from the top of a tower 40 m high with a velocity of 10 m//s. Find the time when it strikes the ground. Take g=10 m//s^2 .

A ball is dropped from the top of a building the ball takes 0.5 s to fall past the 3 m length of a window at certain distance from the top of the building. Speed of the ball as it crosses the top edge of the window is (g=10 m//s^(2))

A particle of mass 50 g is projected horizontally from the top of a tower of height 50 m with a velocity 20m//s . If g=10m//s^(2) , then find the :-