A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
ALLEN -CIRCULAR MOTION-EXERCISE(O-1)
- The value of n so that vectors 2hati+3hatj-2hatk, 5hati+nhatj+hatk and...
Text Solution
|
- If a and b are two vectors.then the value of (a+b)xx(a-b) is
Text Solution
|
- "|"oversetrightarrow(a).oversetrightarrow(b)"|"=sqrt3"|"oversetrightar...
Text Solution
|
- A body is executing circular motion in the vertical plane containing d...
Text Solution
|
- If the magnitude of velocity in the previous question is decreasing wi...
Text Solution
|
- The direction of angular acceleration of a body moving in a circle in ...
Text Solution
|
- The second's hand of a watch has length 6 cm. Speed of end point and m...
Text Solution
|
- A point P moves in counter clockwise direction on a circular path as s...
Text Solution
|
- A spot light S rotates in a horizontal plane with a constant angular v...
Text Solution
|
- Which of the following statements is FALSE for a paricle moving in a...
Text Solution
|
- A particle is moving in a circle:
Text Solution
|
- A particle of mass m is tied to light string and rotated with a speed ...
Text Solution
|
- Which vector in the figures best represents the acceleration of a pend...
Text Solution
|
- A conical pendulum is moving in a circle with angular velocity omega. ...
Text Solution
|
- A point mass m is suspended from a light thread of length l, fixed at ...
Text Solution
|
- A long horizontal rod has a bead which can slide along its length and ...
Text Solution
|
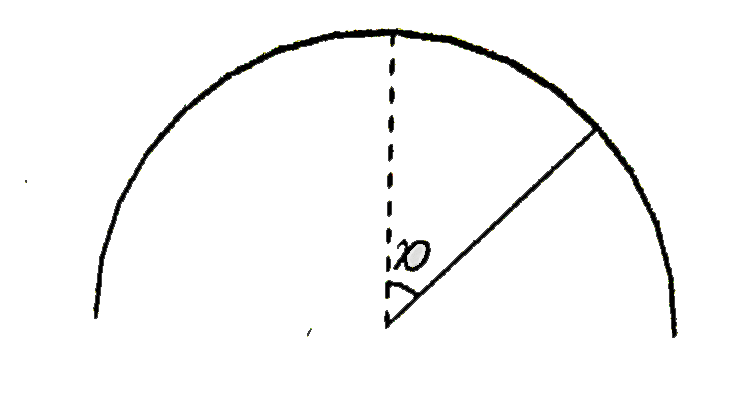
- An insect crawls up a hemispherical surface very slowly (see the figur...
Text Solution
|
- The maximum velocity (in ms^(-1)) with which a car driver must travers...
Text Solution
|
- A particle is acted upon by a force of constant magnitude which is alw...
Text Solution
|
- A car runs around a curve of radius 10m at a constant speed of 10ms^(-...
Text Solution
|