A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
ALLEN -CIRCULAR MOTION-EXERCISE(O-2)
- A ring of radius 'r' and mass per unit length 'm' rotates with an angu...
Text Solution
|
- A uniform rod of mass m and length l rotates in a horizontal plane wit...
Text Solution
|
- The magnitude of displacement of a particle moving in a circle of radi...
Text Solution
|
- A traffic policeman standing at the intersection sees 2 cars A & B tur...
Text Solution
|
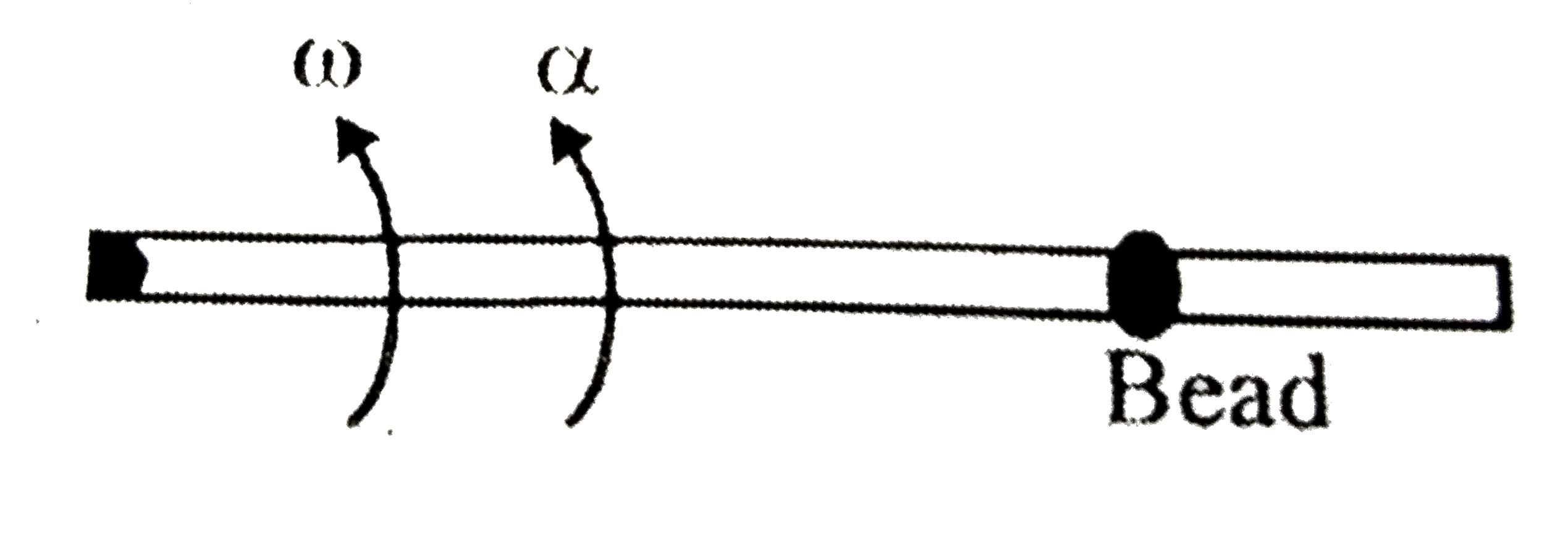
- A bead is contrained to move on rod in granvity free space as shown in...
Text Solution
|
- A particle is moving in a circular path. The acceleration and moment o...
Text Solution
|
- A particle A moves along a circle of radius R=50cm so that its radius ...
Text Solution
|