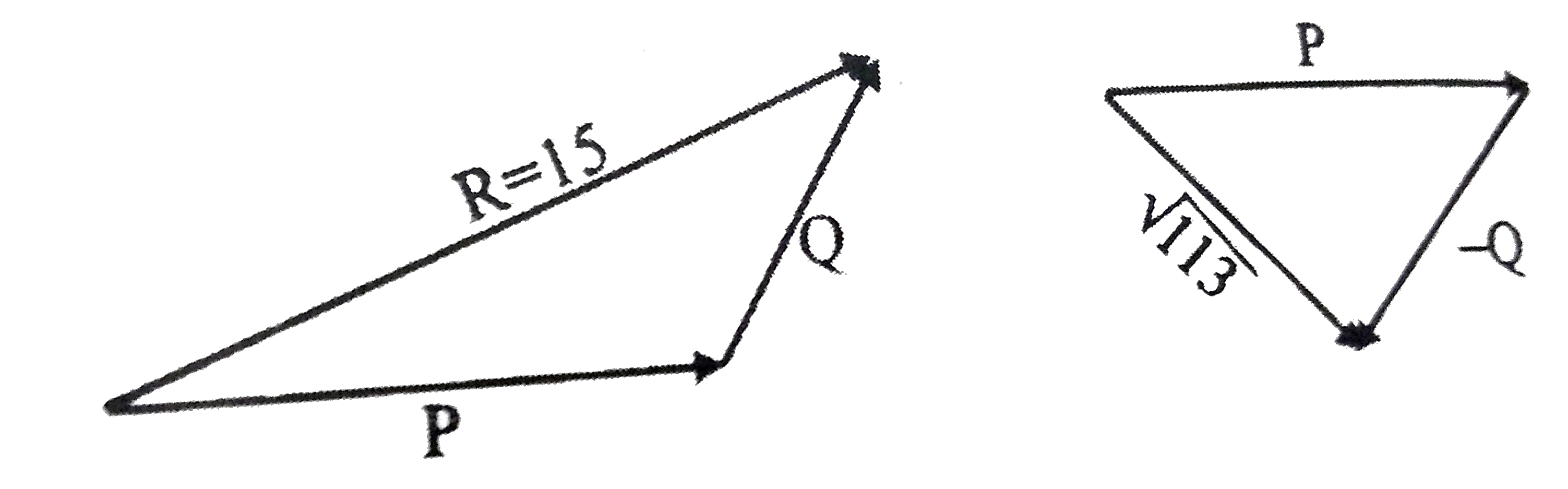
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
UNIT & DIMENSIONS, BASIC MATHS AND VECTOR
ALLEN |Exercise Exercise (S-1)|22 VideosUNIT & DIMENSIONS, BASIC MATHS AND VECTOR
ALLEN |Exercise Exercise (S-2)|7 VideosUNIT & DIMENSIONS, BASIC MATHS AND VECTOR
ALLEN |Exercise Exercise (J-A)|7 VideosTEST PAPERS
ALLEN |Exercise MATHS|1 VideosWAVE OPTICS
ALLEN |Exercise Exercise 2 (Previous Year Questions)|7 Videos
Similar Questions
Explore conceptually related problems
ALLEN -UNIT & DIMENSIONS, BASIC MATHS AND VECTOR -Solved Examples
- Two displacement vectors of same magnitude are arranged in the folllow...
Text Solution
|
- Two vectors vec(P) " and "vec(Q) are added, the magnitude of resulta...
Text Solution
|
- Three forces are acting on a body to make it in equilibrium , which se...
Text Solution
|
- Keeping one vector constant, if direction of other to be added in the ...
Text Solution
|
- If vec(A)=2hati+hatj+hatk " and " vecB=10hati+5hatj+5hatk, if the magn...
Text Solution
|
- The component of vec(A)=hat(i)+hat(j)+5hat(k) perpendicular to vec(B)=...
Text Solution
|
- Solve the equation 3x^(2)+ 5x+2=0 find the roots.
Text Solution
|