Home
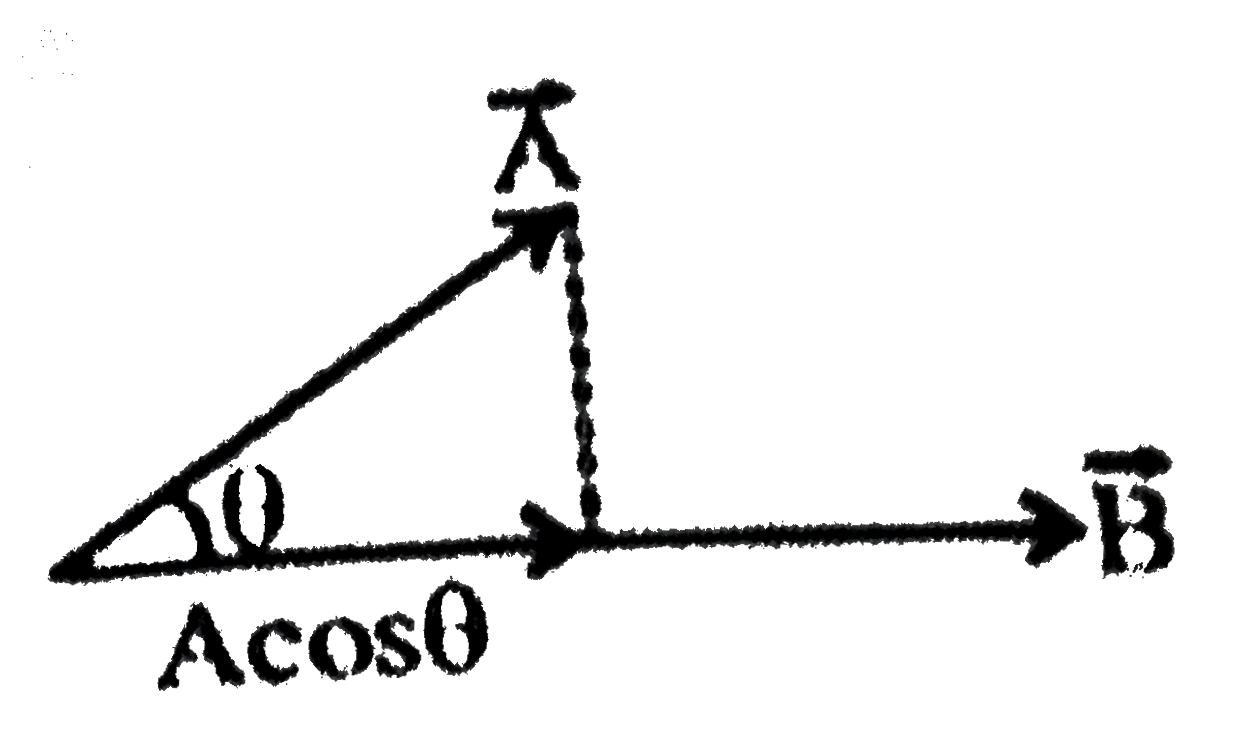
Class 12
PHYSICS
The component of vec(A)=hat(i)+hat(j)+5h...

The component of `vec(A)=hat(i)+hat(j)+5hat(k)` perpendicular to `vec(B)=3hat(i)+4hat(j)` is

A

`-(4)/(25)hati+(3)/(25)hatj+5hatk`

B

`-(8)/(25)hati-(6)/(25)hatj+5hatk`

C

`(4)/(25)hati-(3)/(25)hatj+5hatk`

D

`+(8)/(25)hati-(6)/(25)hatj+5hatk`

Text Solution

Verified by Experts

The correct Answer is:
C

`vec(A)_(||)=A cos theta=A((vecA.vec(B))/(AB))`
`=(vecA.vec(B))/(B)=(3+4)/(5)=(7)/(5)`
`vec(A)_(||)=(7)/(5)((3hati+4hatj)/(5))=(7)/(25)(3hati+4hatj)`
`vec(A)_(||)=(21)/(25)hati+(28)/(25)hatj`
`vec(A)_(bot)=(hati+hatj+5hatk)=((21)/(25)hati+(28)/(25)hatj)`
`=(4)/(25)hati-(3)/(25)hatj+5hatk`
Promotional Banner

Topper's Solved these Questions

  • UNIT & DIMENSIONS, BASIC MATHS AND VECTOR

    ALLEN |Exercise Exercise (S-1)|22 Videos

  • UNIT & DIMENSIONS, BASIC MATHS AND VECTOR

    ALLEN |Exercise Exercise (S-2)|7 Videos

  • UNIT & DIMENSIONS, BASIC MATHS AND VECTOR

    ALLEN |Exercise Exercise (J-A)|7 Videos

  • TEST PAPERS

    ALLEN |Exercise MATHS|1 Videos

  • WAVE OPTICS

    ALLEN |Exercise Exercise 2 (Previous Year Questions)|7 Videos

Similar Questions

Explore conceptually related problems

The compenent of vec(A)=hat(i)+hat(j)+5hat(j) perpendicular to vec(B)=3hat(i)+4hat(j) is

The unit vactor parallel to the resultant of the vectors vec(A)=4hat(i)+3hat(j)+6hat(k) and vec(B)=-hat(i)+3hat(j)-8hat(k) is :-

Find the components of vector vec(a)=3hat(i)+4hat(j) along the direction of vectors hat(i)+hat(j) & hat(i)-hat(j)

Find the angle between vec(P) = - 2hat(i) +3 hat(j) +hat(k) and vec(Q) = hat(i) +2hat(j) - 4hat(k)

If the angle between vec(A) = 2hat(i)+4hat(j)+2hat(k) and vec(B) =2hat(i) +hat(k) " is " 30^(@) , then find the projection of vec(B ) on A .

Find the angle between force vec(F) =(3hat(i)+4hat(j)-5hat(k)) unit and displacement vec(d)=(5hat(i)+4hat(j)+3hat(k)) unit , Also find the projection of F on d .

Consider three vectors vec(A)=2 hat(i)+3 hat(j)-2 hat(k)" " vec(B)=5hat(i)+nhat(j)+hat(k)" " vec(C)=-hat(i)+2hat(j)+3 hat(k) If these three vectors are coplanar, then value of n will be

If vec(A) =2hat(i)-2hat(j) and vec(B)=2hat(k) then vec(A).vec(B) ……

Angle between the vectors vec(a)=-hat(i)+2hat(j)+hat(k) and vec(b)=xhat(i)+hat(j)+(x+1)hat(k)

If vectors vec(A)=(hat(i)+2hat(j)+3hat(k))m and vec(B)=(hat(i)-hat(j)-hat(k))m represent two sides of a triangle, then the third side can have length equal to :