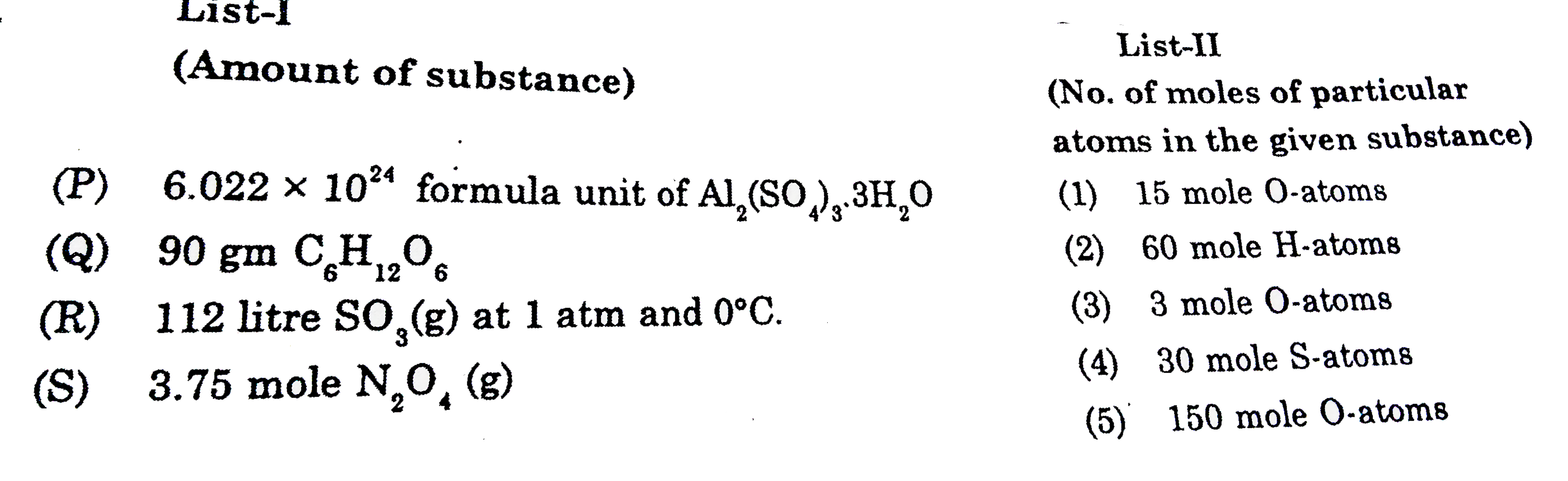A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
ALLEN -TEST PAPER-CHEMISTRY SECTION-I
- Which of the following statements is/are incorrect -
Text Solution
|
- The incorrect statement(s) for 14 gm CO is/are :
Text Solution
|
- Which of the following statement is/are correct for sodium phosphite ?
Text Solution
|
- If we change the central atom from S to Se in SO4^(2-) then which of t...
Text Solution
|
- The correct order is
Text Solution
|
- Which of the following is correctly matched.
Text Solution
|
- The CORRECT option is
Text Solution
|
- The CORRECT option is
Text Solution
|
- The CORRECT option is
Text Solution
|
- The CORRECT option is
Text Solution
|
- Velocity-time graph for a particle, which is moving in straight line i...
Text Solution
|
- A particle is thrown with 50 m/s vertically upward from the ground.Upw...
Text Solution
|
- Two balls are projected simultaneously from the top of a tall building...
Text Solution
|
- Two balls , projected at different times so they don't collide, have t...
Text Solution
|
- An object moves in x-y plane such that it starts from origin with init...
Text Solution
|
- The position vector of a particle is given by vecr=10hati+(20-5t)hatj(...
Text Solution
|
- Acceleration -position graph for a particle moving along x-axis is giv...
Text Solution
|
- A mango is dropped from rest from a height near the surface of earth.W...
Text Solution
|
- Choose the INCORRECT statement.
Text Solution
|
- A particle moves along x-axis in such a way that its x-co-ordinate var...
Text Solution
|