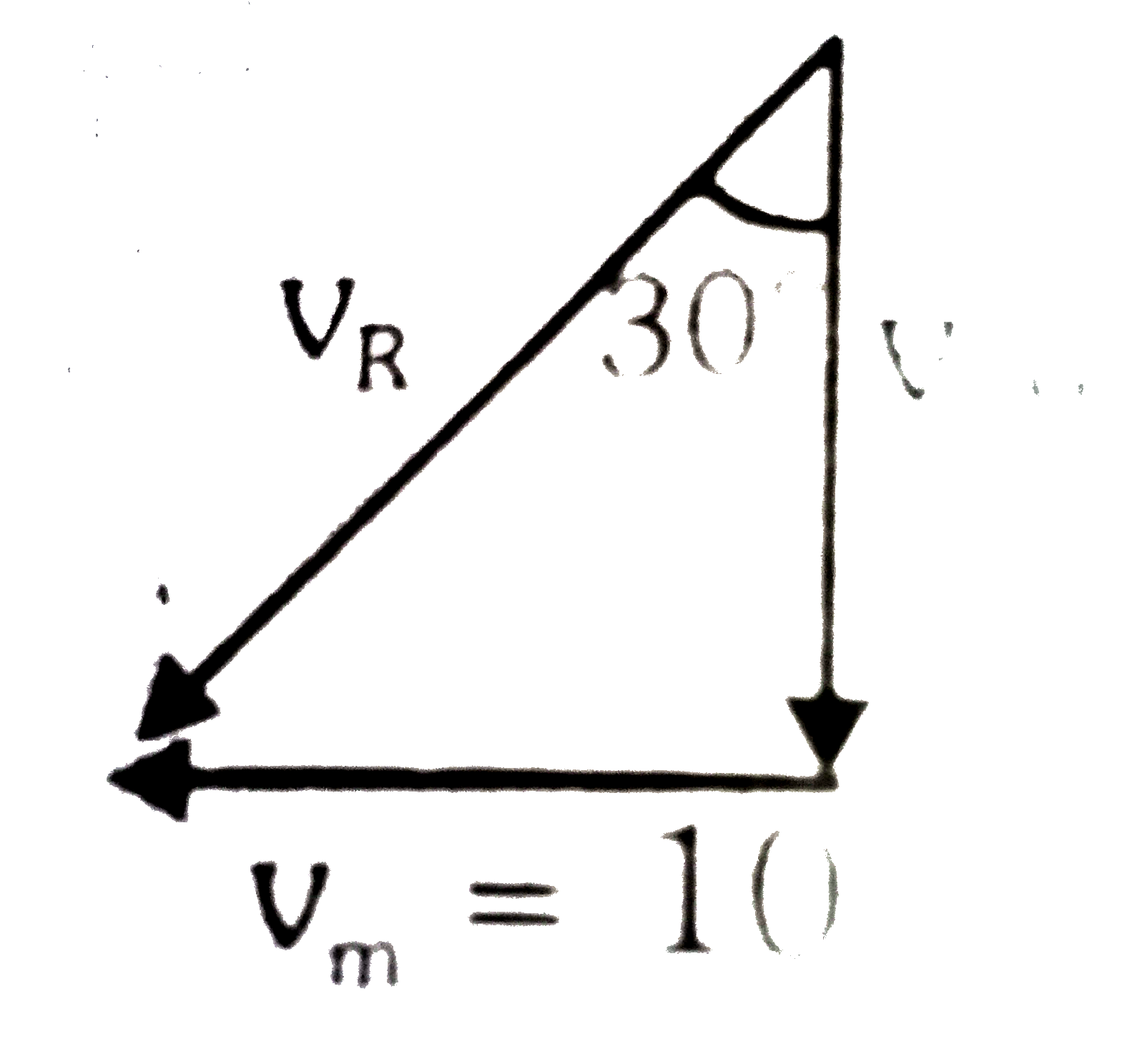Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
ALLEN -MOTION IN A PALNE-Exercise-04[B]
- A boat is moving with a velocity 3 hat i+ 4hat j with respect to groun...
Text Solution
|
- Two cars are moving in the same direction with the same speed 30 km//h...
Text Solution
|
- A stone is thrown upwards and it rises to a height 0f 200m. The relati...
Text Solution
|
- A bus starts moving with acceleration 2 ms^-2. A cyclist 96 m behind t...
Text Solution
|
- A body X is projected upwards with a velocity of 98 ms^(-1), after 4s,...
Text Solution
|
- A bird is flying towards south with a velocity 40km/hr and a train is ...
Text Solution
|
- A train moves in north direction with a speed of 54 km/hr. and a monke...
Text Solution
|
- Two trains each of length 50m. are running with constant speeds on pa...
Text Solution
|
- A bird is flying with a speed of 40 km/hr. in the north direction. A t...
Text Solution
|
- A man is walking on a road with a velocity 3kmhr. Suddenly rain starts...
Text Solution
|
- A boy is runing on the plane road with velocity v with a long hollow t...
Text Solution
|
- A man standing on a road has to hold his umbrella at 30^(@) with the ...
Text Solution
|
- A boat takes 2 hours to travel 8 km and back in still water lake.With ...
Text Solution
|
- A river is flowing at the rate of 6 km/hr. A swimmer swims across with...
Text Solution
|